Logic of Belief Revision
In the logic of belief revision (belief change), a belief state (or database) is represented by a set of sentences. The major operations of change are those consisting in the introduction or removal of a belief-representing sentence. In both cases, changes affecting other sentences may be needed (for instance in order to retain consistency). Rationality postulates for such operations have been proposed, and representation theorems have been obtained that characterize specific types of operations in terms of these postulates.
In the dominant theory of belief revision, the so-called AGM model, the set representing the belief state is assumed to be a logically closed set of sentences (a belief set). One of most debated topics in belief revision theory is the recovery postulate, according to which all the original beliefs are regained if one of them is first removed and then reinserted. The recovery postulate holds in the AGM model but not in closely related models employing belief bases. Another much discussed topic is how repeated changes can be adequately represented. Several alternative models have been proposed that are intended to provide a more realistic account of belief change than that offered by the AGM model.
- 1. Introduction
- 2. Contraction
- 3. Revision
- 4. Possible world modelling
- 5. Belief bases
- 6. Other operations
- 6.1 Update
- 6.2 Consolidation
- 6.3 Semi-revision
- 6.4 Selective revision
- 6.5 Shielded contraction
- 6.6 Replacement
- 6.7 Merge
- 6.8 Multiple contraction and revision
- 6.9 Indeterministic belief change
- 6.10 Operations for an extended language
- 6.11 Changes in the strength of beliefs
- 6.12 Changes in norms and preferences
- 7. Iterated change
- 8. Alternative accounts
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Introduction
1.1 History
Belief revision (belief change, belief dynamics) has been recognized as a subject of its own since the middle of the 1980s. It grew out of two converging research traditions.
One of these emerged in computer science. Since the beginning of computing, programmers have developed procedures by which databases can be updated. The development of Artificial Intelligence inspired computer scientists to construct more sophisticated models of database updating. The truth maintenance systems developed by Jon Doyle (1979) were important in this development. One of the most significant theoretical contributions was a 1983 paper by Ronald Fagin, Jeffrey Ullman and Moshe Vardi, in which they introduced the notion of database priorities.
The second of these two research traditions is philosophical. In a wide sense, belief change has been a subject of philosophical reflection since antiquity. In the twentieth century, philosophers have discussed the mechanisms by which scientific theories develop, and they have proposed criteria of rationality for revisions of probability assignments. Beginning in the 1970s, a more focused discussion has taken place on the requirements of rational belief change. Two milestones can be pointed out. The first was a series of studies conducted by Isaac Levi in the 1970s (Levi 1977, 1980). Levi posed many of the problems that have since then been major concerns in this field of research. He also provided much of the basic formal framework. William Harper’s (1977) work from the same period has also had a lasting influence.
The next milestone was the AGM model, so called after its three originators, Carlos Alchourrón, Peter Gärdenfors, and David Makinson (1985). Alchourrón and Makinson had previously cooperated in studies of changes in legal codes (Alchourrón and Makinson 1981, 1982). Gärdenfors’s early work was concerned with the connections between belief change and conditional sentences (Gärdenfors 1978, 1981). With combined forces the three wrote a paper that provided a new, much more general and versatile formal framework for studies of belief change. (On the history of their joint work, see Makinson 2003 and Gärdenfors 2011.) Since the paper was published in the Journal of Symbolic Logic in 1985, its major concepts and constructions have been the subject of significant elaboration and development. The AGM model and developments that have grown out of it still form the core of belief revision theory.
1.2 The representation of beliefs and changes
In the AGM model and most other models of belief change, beliefs are represented by sentences in some formal language. Sentences do not capture all aspects of belief, but they are the best general-purpose representation that is presently available.
The beliefs held by an agent are represented by a set of such belief-representing sentences. It is usually assumed that this set is closed under logical consequence, i.e., every sentence that follows logically from this set is already in the set. This is clearly an unrealistic idealization, since it means that the agent is taken to be “logically omniscient”, i.e. a perfect logical reasoner. However, it is a useful idealization since it simplifies the logical treatment; indeed, it seems difficult to obtain an interesting formal treatment without it. In logic, logically closed sets are called “theories”. In formal epistemology they are also called “corpora”, “knowledge sets”, or (more commonly) “belief sets”.
Isaac Levi (1991) has clarified the nature of this idealization by pointing out that a belief set consists of the sentences that someone is committed to believe, not those that she actually believes in. According to Levi, we are doxastically committed to believe in all the logical consequences of our beliefs, but typically our performance does not live up to this commitment. The belief set is the set of the agent’s epistemic commitments, and therefore larger than the set of her actually held beliefs.
In the AGM framework, there are three types of belief change. In contraction, a specified sentence \(p\) is removed, i.e., a belief set \(K\) is superseded by another belief set \(K\div p\) that is a subset of \(K\) not containing \(p\). In expansion a sentence \(p\) is added to \(K\), and nothing is removed, i.e. \(K\) is replaced by a set \(K+p\) that is the smallest logically closed set that contains both \(K\) and \(p\). In revision a sentence \(p\) is added to \(K\), and at the same time other sentences are removed if this is needed to ensure that the resulting belief set \(K* p\) is consistent.
It is important to note the specific character of these models. They are input-assimilating. This means that the object of change, the belief set, is exposed to an input, and is changed as a result of this. No explicit representation of time is included. Instead, the characteristic mathematical constituent is a function that, to each pair of a belief set and an input, assigns a new belief set.
1.3 Formal preliminaries
The belief-representing sentences form a language. (As is usual in logic, the language is identified with the set of all sentences it contains.) Sentences, i.e. elements of this language, will be represented by lowercase letters \((p, q\ldots)\) and sets of sentences by capital letters. This language contains the usual truth-functional connectives: negation \((\neg)\), conjunction \((\amp)\), disjunction \((\vee)\), implication \((\rightarrow)\), and equivalence (\(\leftrightarrow\)). \(\smbot\) denotes an arbitrary contradiction (“falsum”), and \(\smtop\) an arbitrary tautology.
To express the logic, a Tarskian consequence operator will be used. Intuitively speaking, for any set \(A\) of sentences, \(\Cn(A)\) is the set of logical consequences of \(A\). More formally, a consequence operation on a given language is a function \(\Cn\) from sets of sentences to sets of sentences. It satisfies the following three conditions:
Inclusion:
\(A\subseteq \Cn(A)\)
Monotony:
If \(A\subseteq B\), then \(\Cn(A) \subseteq \Cn(B)\)
Iteration:
\(\Cn(A) = \Cn(\Cn(A))\)
\(\Cn\) is assumed to be supraclassical, i.e. if \(p\) can be derived from \(A\) by classical truth-functional logic, then \(p \in \Cn(A)\). \(A\) is a belief set if and only if \(A = \Cn(A)\). In what follows, \(K\) will denote a belief set. \(X \vdash p\) is an alternative notation for \(p \in \Cn(X)\), and \(X \not\vdash p\) for \(p \not\in \Cn(X)\). \(\Cn(\varnothing)\) is the set of tautologies.
The expansion of \(K\) by a sentence \(p\), i.e. the operation that just adds \(p\) and removes nothing, is denoted \(K+p\) and defined as follows: \(K+p = \Cn(K\cup \{p\})\).
2. Contraction
2.1 Partial meet contraction
The outcome of contracting \(K\) by \(p\) should be a subset of \(K\) that does not imply \(p\), but from which no elements of \(K\) have been unnecessarily removed. Therefore, it is of interest to consider the inclusion-maximal subsets of \(K\) that do not imply \(p\).
For any set \(A\) and sentence \(p\) the remainder set \(A\bot p\) (“\(A\) remainder \(p\)”) is the set of inclusion-maximal subsets of \(A\) that do not imply \(p\). In other words, a set \(B\) is an element of \(A\bot p\) if and only if it it is a subset of \(A\) that does not imply \(p\), and there is no set \(B'\) not implying \(p\) such that \(B\subset B'\subseteq A\). The elements of \(A\bot p\) are called “remainders”.
If the operation of contraction uncompromisingly minimizes information loss, then \(K\div p\) will be one of the remainders. However, this construction can be shown to have implausible properties. A more reasonable recipe for contraction is to let \(K\div p\) be the intersection of some of the remainders. This is partial meet contraction, the major innovation in the classic 1985 paper by Carlos Alchourrón, Peter Gärdenfors and David Makinson. An operation of partial meet contraction employs a selection function that selects the “best” elements of \(K\bot p\). More precisely, a selection function for \(K\) is a function \(\gamma\) such that if \(K\bot p\) is non-empty, then \(\gamma(K\bot p)\) is a non-empty subset of \(K\bot p\). In the limiting case when \(K\bot p\) is empty, then \(\gamma(K\bot p)\) is defined to be equal to \(\{K\}\).
The outcome of the partial meet contraction is equal to the intersection of the set of selected elements of \(K\bot p\), i.e. \(K\div p = \bigcap \gamma(K\bot p)\).
The limiting case when for all sentences \(p\), \(\gamma(K\bot p)\) has exactly one element is called maxichoice contraction. The other limiting case in which \(\gamma(K\bot p) = K\bot p\) whenever \(K\bot p\) is non-empty is called full meet contraction. Both limiting cases are technically useful, but they also both have highly unrealistic properties.
Partial meet contraction of a belief set satisfies six postulates that are called the basic Gärdenfors postulates (or basic AGM postulates). To begin with, when a belief set \(K\) is contracted by a sentence \(p\), the outcome should be logically closed.
Closure:
\(K\div p = \Cn(K\div p)\)
Contraction should be successful, i.e., \(K\div p\) should not imply \(p\) (or not contain \(p\), which is the same thing if Closure is satisfied). However, it would be too much to require that \(p \not\in \Cn(K\div p)\) for all sentences \(p\), since it cannot hold if \(p\) is a tautology. The success postulate has to be conditional on \(p\) not being logically true.
Success:
If \(p \not\in \Cn(\varnothing)\), then \(p \not\in \Cn(K\div p)\).
The Success postulate has been put in doubt since there may be sentences other than tautologies that an epistemic agent may refuse to withdraw. (On operations that do not satisfy Success, see Section 6.5.)
The contracted set is assumed to be a subset of the original one:
Inclusion:
\(K\div p \subseteq K\)
Inclusion is usually considered to be a constitutive property of contraction. However, it has also been questioned with the argument that when the epistemic agent ceases to believe in \(p\), then this is usually because she receives some new information that contradicts \(p\). Arguably, that information should be included in \(K\div p\).
If the sentence to be contracted is not included in the original belief set, then contraction by that sentence involves no change at all. Such contractions are idle (vacuous) operations, and they should leave the original set unchanged.
Vacuity:
If \(p \not\in \Cn(K)\), then \(K\div p = K\).
Logically equivalent sentences should be treated alike in contraction:
Extensionality:
If \(p\leftrightarrow q \in \Cn(\varnothing)\), then \(K\div p = K\div
q\).
Extensionality guarantees that the logic of contraction is extensional in the sense of allowing logically equivalent sentences to be freely substituted for each other.
Belief contraction should not only be successful, it should also be minimal in the sense of leading to the loss of as few previous beliefs as possible. The epistemic agent should give up beliefs only when forced to do so, and should then give up as few of them as possible. This is ensured by the following postulate:
Recovery:
\(K \subseteq (K\div p)+p\)
According to Recovery, so much is retained after \(p\) has been removed that everything will be recovered by reinclusion (through expansion) of \(p\).
One of the central results about the AGM model is a representation theorem for partial meet contraction. According to this theorem, an operation \(\div\) is a partial meet contraction for a belief set \(K\) if and only if it satisfies the six above-mentioned postulates, namely Closure, Success, Inclusion, Vacuity, Extensionality, and Recovery.
A selection function for a belief set \(K\) should, for all sentences \(p\), select those elements of \(K\bot p\) that are “best”, or most worth retaining. However, the definition of a selection function is very general, and allows for quite disorderly selection patterns. An orderly selection function should always choose the best element(s) of the remainder set according to some well-behaved preference relation. A selection function \(\gamma\) for a belief set \(K\) is relational if and only if there is a binary relation \(\mathbf{R}\) such that for all sentences \(p\), if \(K\bot p\) is non-empty, then \(\gamma(K\bot p) = \{B \in K\bot p \mid C\mathbf{R}B\) for all \(C \in K\bot p\}\). Furthermore, if \(\mathbf{R}\) is transitive (i.e., it satisfies: If \(A\mathbf{R}B\) and \(B\mathbf{R}C\), then \(A\mathbf{R}C)\), then \(\gamma\) and the partial meet contraction that it gives rise to are transitively relational.
In order to characterize transitively relational partial meet contraction, postulates are needed that refer to contraction by conjunctions.
In order to give up a conjunction \(p \amp q\), the agent must relinquish either her belief in \(p\) or her belief in \(q\) (or both). Suppose that contracting by \(p \amp q\) leads to loss of the belief in \(p\), i.e., that \(p \not\in K\div(p \amp q)\). It can be expected that in this case contraction by \(p \amp q\) should lead to the loss of all beliefs that would have been lost in order to contract by \(p\). Another way to express this is that everything that is retained in \(K\div(p \amp q)\) is also retained in \(K\div p\):
Conjunctive inclusion:
If \(p \not\in K\div(p \amp q)\), then \(K\div(p \amp q) \subseteq
K\div p\).
Another fairly reasonable principle for contraction by conjunctions is that whatever can withstand both contraction by \(p\) and contraction by \(q\) can also withstand contraction by \(p \amp q\). In other words, whatever is an element of both \(K\div p\) and \(K\div q\) is also an element of \(K\div(p \amp q)\).
Conjunctive overlap:
\((K\div p) \cap (K\div q) \subseteq K\div(p \amp q)\)
Conjunctive overlap and Conjunctive inclusion are commonly called Gärdenfors’s supplementary postulates for belief contraction. An operation \(\div\) for \(K\) is a transitively relational partial meet contraction if and only if it satisfies the six basic postulates and in addition both Conjunctive overlap and Conjunctive inclusion.
2.2 Entrenchment-based contraction
When forced to give up previous beliefs, the epistemic agent should give up beliefs that have as little explanatory power and overall informational value as possible. As an example of this, in the choice between giving up beliefs in natural laws and beliefs in single factual statements, beliefs in the natural laws, that have much higher explanatory power, should in general be retained. This was the basic idea behind Peter Gärdenfors’s proposal that contraction of beliefs should be ruled by a binary relation, epistemic entrenchment. (Gärdenfors 1988, Gärdenfors and Makinson 1988) To say of two elements \(p\) and \(q\) of the belief set that “\(q\) is more entrenched than \(p\)” means that \(q\) is more useful in inquiry or deliberation, or has more “epistemic value” than \(p\). In belief contraction, the beliefs with the lowest entrenchment should be the ones that are most readily given up.
The following symbols will be used for epistemic entrenchment:
\(p\le q : p\) is at most as entrenched as \(q\).
\(p\lt q : p\) is less entrenched than \(q\). \(((p\le q) \amp \neg(q\le p)))\)
\(p\equiv q : p\) and \(q\) are equally entrenched. \(((p\le q) \amp(q\le p))\)
Gärdenfors has proposed the following five postulates for epistemic entrenchment. They are often referred to as the standard postulates for entrenchment:
Transitivity:
If \(p\le q\) and \(q\le r\), then \(p\le r\).
Dominance:
If \(p \vdash q\), then \(p\le q\).
Conjunctiveness:
Either \(p\le(p \amp q)\) or \(q\le(p \amp q)\).
Minimality:
If the belief set \(K\) is consistent, then \(p \not\in K\) if and
only if \(p\le q\) for all \(q\).
Maximality:
If \(q\le p\) for all \(q\), then \(p \in \Cn(\varnothing)\).
It follows from the first three of these postulates that an entrenchment relation satisfies connectivity (completeness), i.e. it holds for all \(p\) and \(q\) that either \(p\le q\) or \(q\le p\).
An entrenchment relation \(\le\) gives rise to an operation \(\div\) of entrenchment-based contraction according to the following definition:
\(q \in K\div p\) if and only if \(q \in K\) and either \(p \lt(p \vee q)\) or \(p \in \Cn(\varnothing)\).
Entrenchment-based contraction has been shown to coincide exactly with transitively relational partial meet contraction. For a thorough discussion and more results on entrenchment relations, see Rott 2001.
2.3 Recovery and its avoidance
Recovery is the most debated postulate of belief change. It is easy to find examples that seem to validate Recovery. A person who first loses and then regains her belief that she has a dollar in her pocket seems to return to her previous state of belief. However, other examples can also be presented, in which Recovery yields implausible results. The following are two of the examples that have been offered to show that Recovery does not hold in general:
-
I have read in a book about Cleopatra that she had both a son and a daughter. My set of beliefs therefore contains both \(p\) and \(q\), where \(p\) denotes that Cleopatra had a son and \(q\) that she had a daughter. I then learn from a knowledgeable friend that the book is in fact a historical novel. After that I contract \(p\vee q\) from my set of beliefs, i.e., I do not any longer believe that Cleopatra had a child. Soon after that, however, I learn from a reliable source that Cleopatra had a child. It seems perfectly reasonable for me to then add \(p\vee q\) to my set of beliefs without also reintroducing either \(p\) or \(q\). This contradicts Recovery.
-
I previously entertained the two beliefs “George is a criminal” \((p)\) and “George is a mass murderer” \((q)\). When I received information that induced me to give up the first of these beliefs \((p)\), the second \((q)\) had to go as well (since \(p\) would otherwise follow from \(q)\).
I then received new information that made me accept the belief “George is a shoplifter” \((r)\). The resulting new belief set is the expansion of \(K\div p\) by \(r\), \((K\div p)+r.\) Since \(p\) follows from \(r\), \((K\div p)+p\) is a subset of \((K\div p)+r\). By recovery, \((K\div p)+p\) includes \(q\), from which follows that \((K\div p)+r\) includes \(q\).
Thus, since I previously believed George to be a mass murderer, it follows from Recovery that I cannot after that believe him to be a shoplifter without believing him to be a mass murderer.
Due to the problematic nature of this postulate, it should be interesting to find intuitively less controversial postulates that prevent unnecessary losses in contraction. The following is an attempt to do that:
Core-retainment:
If \(q \in K\) and \(q \not\in K\div p\), then there is a belief set
\(K'\) such that \(K' \subseteq K\) and that \(p \not\in K'\) but \(p
\in K'+q\).
Core-retainment requires of an excluded sentence \(q\) that it in some way contributes to the fact that \(K\) implies \(p\). It gives the impression of being weaker and more plausible than Recovery. However, it has been shown that if an operator \(\div\) for a belief set \(K\) satisfies Core-retainment, then it satisfies Recovery.
Attempts have been made to construct operations of contraction on belief sets that do not satisfy Recovery. Arguably, the most plausible of these constructions is the operation of severe withdrawal that has been thoroughly investigated by Hans Rott and Maurice Pagnucco (2000). It can be constructed from an operation of epistemic entrenchment by modifying the definition as follows:
\(q \in K\div p\) if and only if \(q \in K\) and either \(p \lt q\) or \(p \in \Cn(\varnothing)\).
Severe withdrawal has interesting features, but it also has the following property:
Expulsiveness:
If \(p \not\in \Cn(\varnothing)\) and \(q \not\in \Cn(\varnothing)\)
then either \(p \not\in K\div q\) or \(q \not\in K\div p\).
This is a highly implausible property of belief contraction, since it does not allow unrelated beliefs to be undisturbed by each other’s contraction. Consider a scholar who believes that her car is parked in front of the house. She also believes that Shakespeare wrote the Tempest. It should be possible for her to give up the first of these beliefs while retaining the second. She should also be able to give up the second without giving up the first. Expulsiveness does not allow this. The construction of a plausible operation of contraction for belief sets that does not satisfy Recovery is still an open issue.
3. Revision
The two major tasks of an operation \(*\) of revision are (1) to add the new belief \(p\) to the belief set \(K\), and (2) to ensure that the resulting belief set \(K* p\) is consistent (unless \(p\) is inconsistent). The first task can be accomplished by expansion by \(p\). The second can be accomplished by prior contraction by its negation \(\neg p\). If a belief set does not imply \(\neg p\), then \(p\) can be added to it without loss of consistency. This composition of suboperations gives rise to the following definition of revision (Gärdenfors 1981, Levi 1977):
Levi identity:
\(K* p = (K\div \neg p)+p\).
If \(\div\) is a partial meet contraction, then the operation \(*\) that is defined in this way is a partial meet revision. This is the standard construction of revision in the AGM model.
Partial meet revision has been axiomatically characterized. An operation \(*\) is a partial meet revision if and only if it satisfies the following six postulates:
Closure:
\(K* p = \Cn(K* p)\)
Success:
\(p \in K* p\)
Inclusion:
\(K* p \subseteq K+p\)
Vacuity:
If \(\neg p \not\in K\), then \(K* p = K+p\).
Consistency:
\(K* p\) is consistent if \(p\) is consistent.
Extensionality:
If \((p \leftrightarrow q) \in \Cn(\varnothing)\), then \(K* p = K*
q\).
These six postulates are commonly called the basic Gärdenfors postulates for revision. The most controversial of them is Success. It implies that in response to an inconsistent input sentence, the epistemic agent will acquire an inconsistent belief set, according to which she holds all sentences to be true. Even for consistent input sentences, Success is contestable. It is not implausible for an epistemic agent to consider some statements to be so implausible that nothing can make her believe in them. For belief revision models that do not satisfy Success, see section 6.3. and 6.4.
The following two supplementary postulates are parts of the standard repertoire:
Superexpansion:
\(K* (p \amp q) \subseteq(K* p)+q\)
Subexpansion:
If \(\neg q \not\in \Cn(K* p)\), then \((K* p)+q \subseteq K* (p \amp
q)\).
These postulates are closely related to the supplementary postulates for contraction. Let \(*\) be the partial meet revision defined from the partial meet contraction \(\div\) via the Levi identity. Then \(*\) satisfies superexpansion if and only if \(\div\) satisfies conjunctive overlap. Furthermore, \(*\) satisfies subexpansion if and only if \(\div\) satisfies conjunctive inclusion.
The following postulate was introduced by Hans Rott:
Disjunctive factoring:
\(K* (p\vee q) \) is equal to one of \(K* p\), \(K* q\), and \(K*
p\cap K* q\).
Rott showed that in the presence of the six basic AGM postulates, the two supplementary AGM postulates, Superexpansion and Subexpansion, both hold if and only if Disjunctive factoring holds.
4. Possible world modelling
Alternative models of belief states can be constructed out of sets of possible worlds (Grove 1988). In logical parlance, by a possible world is meant a maximal consistent subset of the language. By a proposition is meant a set of possible worlds. There is a one-to-one correspondence between propositions and belief sets. Each belief set can be represented by the proposition (set of possible worlds) that consists of those possible worlds that contain the belief set in question.
For any set \(A\) of sentences, let \([A]\) denote the set of possible worlds that contain \(A\) as a subset, and similarly for any sentence \(p\) let \([p]\) be the set of possible worlds that contain \(p\) as an element. If \(A\) is inconsistent, then \([A] = \varnothing\). Otherwise, \([A]\) is a non-empty set of possible worlds. (It is assumed that \(\bigcap \varnothing\) is equal to the whole language.) If \(K\) is a belief set, then \(\bigcap[K] = K\).
The propositional account provides an intuitively clear picture of some aspects of belief change. It is convenient to use a geometrical surface to represent the set of possible worlds. In Diagram 1, every point on the rectangle’s surface represents a possible world. The circle marked \([K]\) represents those possible worlds in which all sentences in \(K\) are true, i.e., the set \([K]\) of possible worlds. The area marked \([p]\) represents those possible worlds in which the sentence \(p\) is true.
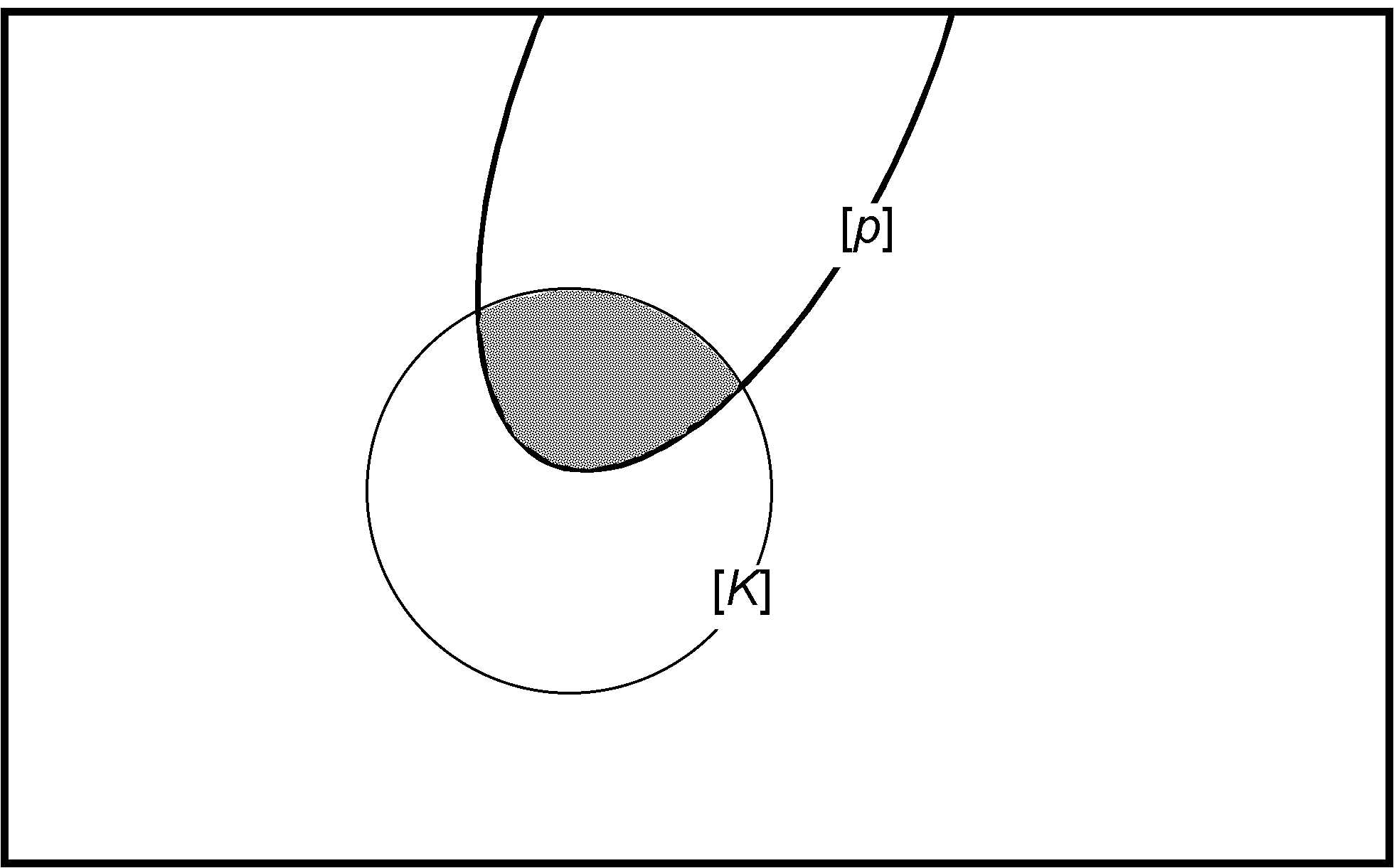
Diagram 1. Revision of \(K\) by \(p\).
In Diagram 1, \([K]\) and \([p]\) have a non-empty intersection, which means that \(K\) is compatible with \(p\). The revision of \(K\) by \(p\) is therefore not belief-contravening. Its outcome is obtained by giving up those elements of \([K]\) that are incompatible with \(p\). In other words, the result of revising \([K]\) by \([p]\) should be equal to \([K]\cap[p]\).
If \([K]\) and \([p]\) do not intersect, then the outcome of the revision must be sought outside of \([K]\), but it should nevertheless be a subset of \([p]\). In general:
The outcome of revising \([K]\) by \([p]\) is a subset of \([p]\) that is
- non-empty if \([p]\) is non-empty
- equal to \([K]\cap[p]\) if \([K]\cap[p]\) is non-empty
This simple rule for revision can be shown to correspond exactly to partial meet revision.
The revised belief state should not differ more from the original belief state \([K]\) than what is motivated by \([p]\). This can be achieved by requiring that the outcome of revising \([K]\) by \([p]\) consists of those elements of \([p]\) that are as close as possible to \([K]\). For that purpose, \([K]\) can be thought of as surrounded by a system of concentric spheres (just as in David Lewis’s account of counterfactual conditionals). Each sphere represents a degree of closeness or similarity to \([K]\).
In this model, the outcome of revising \([K]\) by \([p]\) should be the intersection of \([p]\) with the narrowest sphere around \([K]\) that has a non-empty intersection with \([p]\), as in Diagram 2. This construction was invented by Adam Grove (1988), who also proved that such sphere-based revision corresponds exactly to transitively relational partial meet revision. It follows that it also corresponds exactly to entrenchment-based revision.
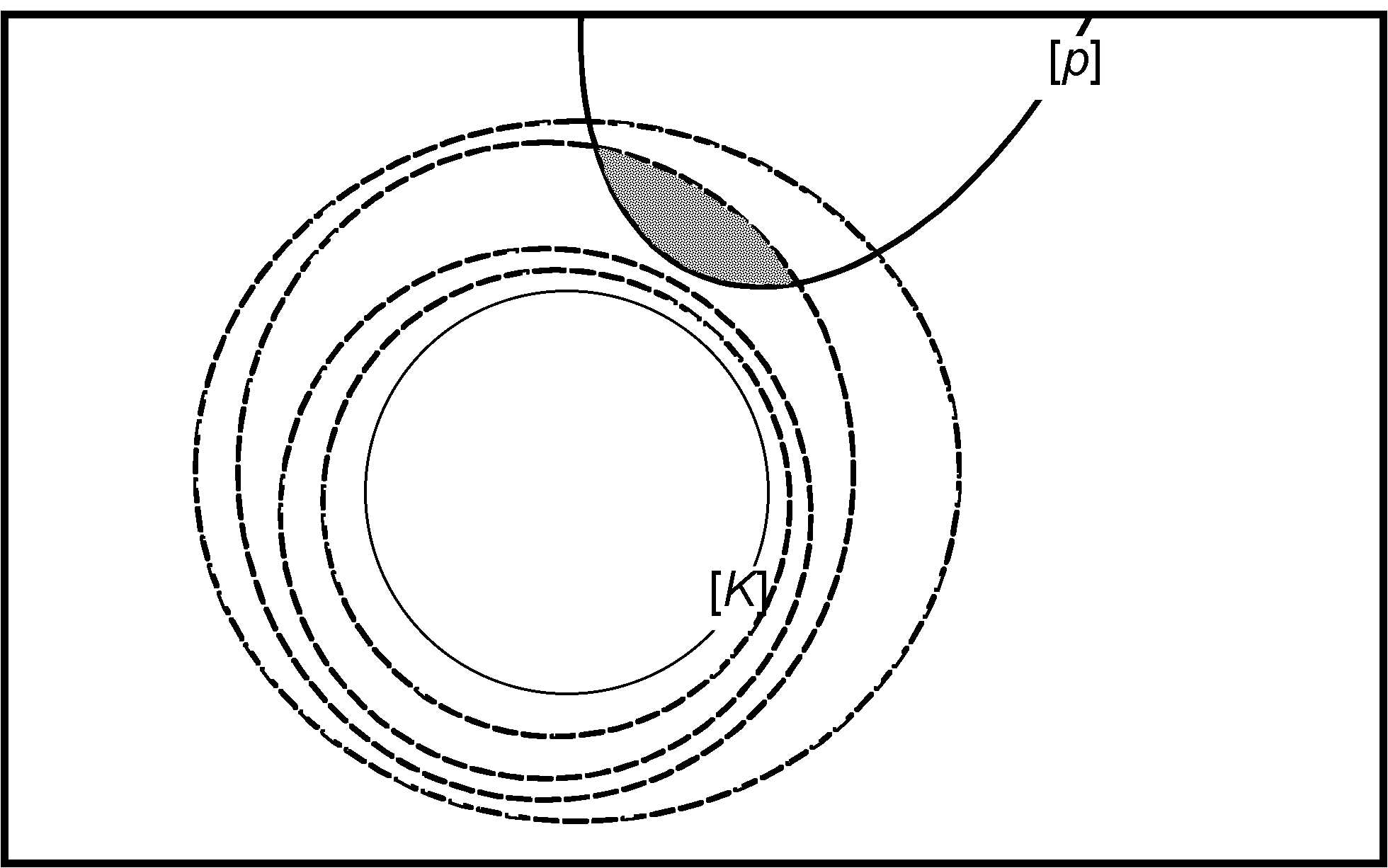
Diagram 2. Sphere-based revision of \(K\) by \(p\).
Possible world models can also be used for contraction. In contraction, a restriction on what worlds are “possible” (compatible with the agent’s beliefs) is removed. Thus, the set of possibilities is enlarged, so that the contraction of \([K]\) by \([p]\) will result in a superset of \([K]\). Furthermore, the new possibilities should be worlds in which \(p\) does not hold, i.e., they should be worlds in which \(\neg p\) holds. In the limiting case when \([K]\) and \([\neg p]\) have a non-empty intersection, no enlargement of \([K]\) is necessary to make \(\neg p\) possible, and the original belief state will therefore be unchanged. In summary, contraction should be performed according to the following rule:
The outcome of contracting \([K]\) by \([p]\) is the union of \([K]\) and a subset of \([\neg p]\) that is
- non-empty if \([\neg p]\) is non-empty
- equal to \([K]\cap[\neg p]\) if \([K]\cap[\neg p]\) is non-empty
Belief-contravening contraction is illustrated in Diagram 3. Contraction performed according to this rule can be shown to correspond exactly to partial meet contraction. Furthermore, the special case when the whole of \([\neg p]\) is added to \([K]\) corresponds exactly to full meet contraction. The other extreme case, when only one element of \([\neg p]\) (a “point” on the surface) is added to \([K]\) corresponds exactly to maxichoice contraction. Thus, in maxichoice contraction by \(p\) only one possible way in which \(p\) can be false \((\neg p\) can be true) is added.
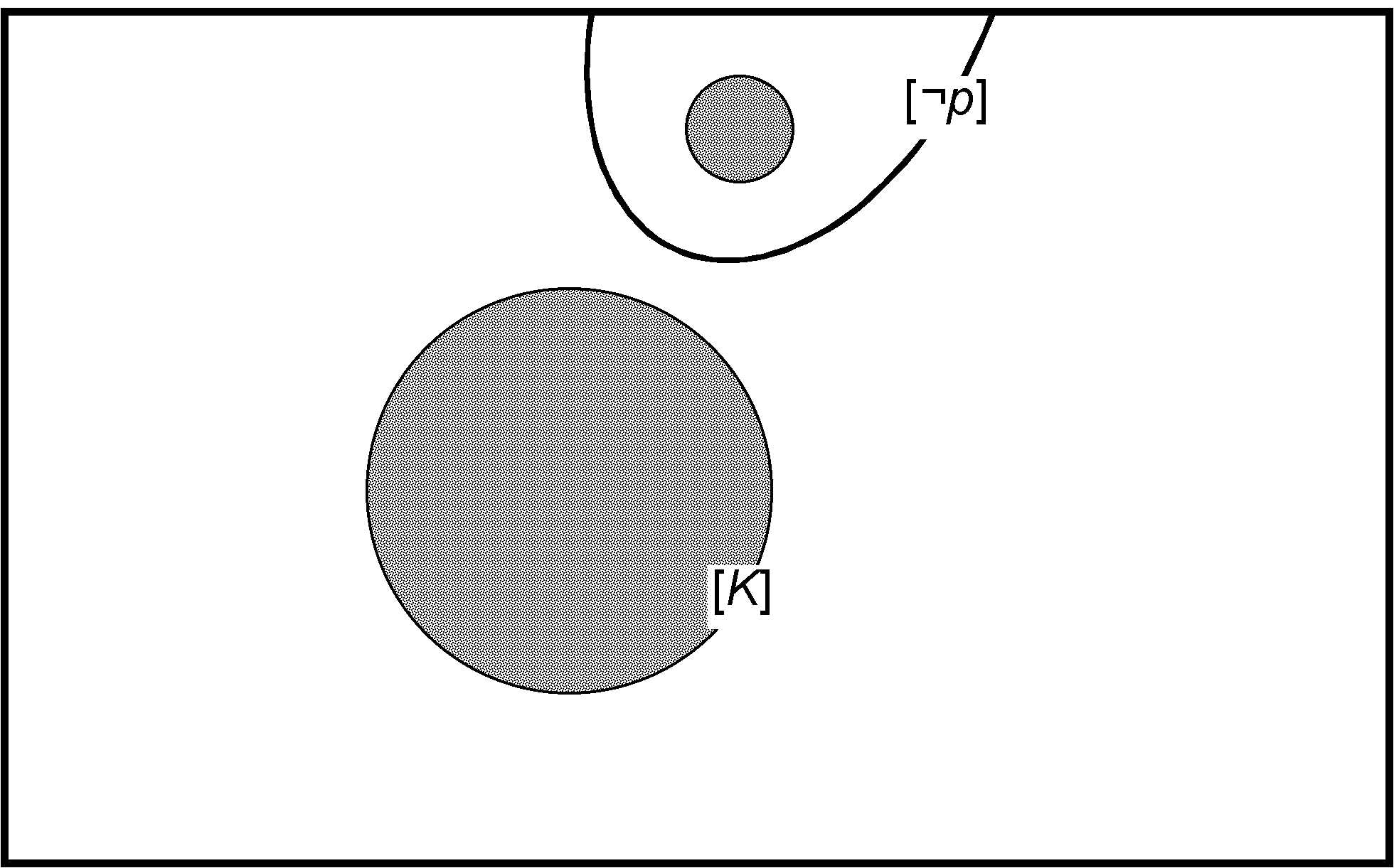
Diagram 3. Contraction of \(K\) by \(p\).
Grove’s sphere systems can also be used for contraction. In sphere-based contraction by \(p\), those elements of \([\neg p]\) are added that belong to the closest sphere around \([K]\) that has a non-empty intersection with \([\neg p]\). The procedure is shown in Diagram 4. Sphere-based contraction corresponds exactly to transitively relational partial meet contraction.
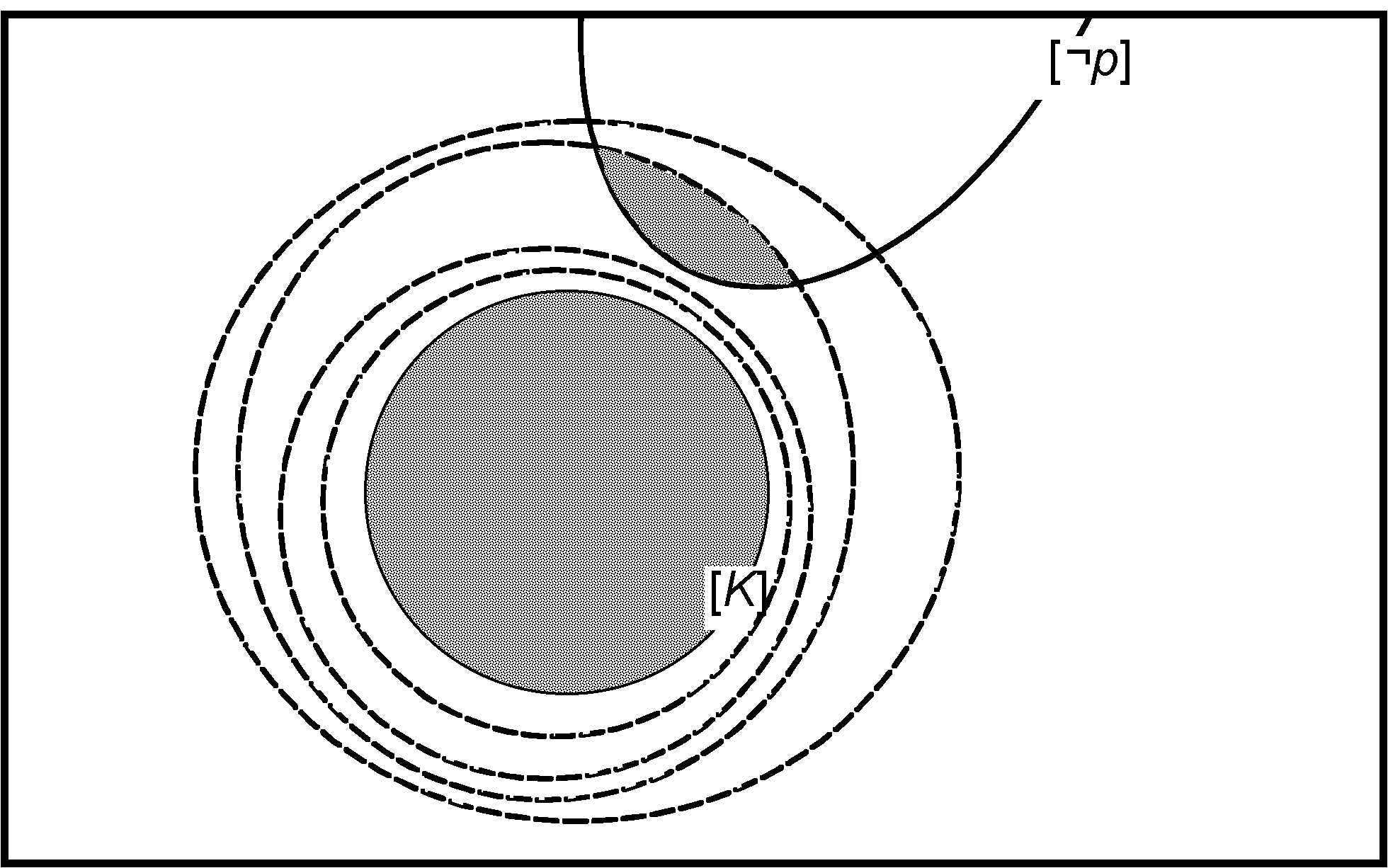
Diagram 4. Sphere-based contraction of \(K\) by \(p\).
5. Belief bases
5.1 Increased expressive power
In the approaches discussed above, all beliefs in the belief set are treated equally in the sense that they are all taken seriously as beliefs in their own right. However, due to logical closure the belief set contains many elements that are not really worth to be taken seriously. Hence, suppose that the belief set contains the sentence \(p\), “Shakespeare wrote Hamlet”. Due to logical closure it then also contains the sentence \(p \vee q\), “Either Shakespeare wrote Hamlet or Charles Dickens wrote Hamlet”. The latter sentence is a “mere logical consequence” that should have no standing of its own.
Belief bases have been introduced to capture this feature of the structure of human beliefs. A belief base is a set of sentences that is not (except as a limiting case) closed under logical consequence. Its elements represent beliefs that are held independently of any other belief or set of beliefs. Those elements of the belief set that are not in the belief base are “merely derived”, i.e., they have no independent standing. In this way, models employing belief bases can be said to achieve a somewhat higher degree of affinity to natural-language doxastic reasoning than what seems to be achievable in models such as AGM that use belief sets as representations of belief sets. (A still higher degree of affinity to natural language can be obtained in models employing hyperintensional logic; see Berto 2019.)
In belief base models, changes are performed on the belief base, which is not logically closed. The underlying intuition is that the merely derived beliefs are not worth retaining for their own sake. If one of them loses the support that it had in basic beliefs, then it will be automatically discarded.
For every belief base \(A\), there is a belief set \(\Cn(A)\) that represents the beliefs held according to \(A\). On the other hand, one and the same belief set can be represented by different belief bases. In this sense, belief bases have more expressive power than belief sets. As an example, the two belief bases \(\{p, q\}\) and \(\{p, p \leftrightarrow q\}\) have the same logical closure. They are therefore statically equivalent, in the sense of representing the same beliefs. On the other hand, the following example shows that they are not dynamically equivalent in the sense of behaving in the same way under operations of change. They can be taken to represent different ways of holding the same beliefs.
Let \(p\) denote that the Liberal Party will support the proposal to subsidize the steel industry, and let \(q\) denote that Ms. Smith, who is a liberal MP, will vote in favour of that proposal.
Abe has the basic beliefs \(p\) and \(q\), whereas Bob has the basic beliefs \(p\) and \(p \leftrightarrow q.\) Thus, their beliefs (on the belief set level) with respect to \(p\) and \(q\) are the same.
Both Abe and Bob receive and accept the information that \(p\) is wrong, and they both revise their belief states to include the new belief that \(\neg p\). After that, Abe has the basic beliefs \(\neg p\) and \(q\), whereas Bob has the basic beliefs \(\neg p\) and \(p \leftrightarrow q\). Now, their belief sets are no longer the same. Abe believes that \(q\) whereas Bob believes that \(\neg q\).
(In belief set models, cases like these are taken care of by assuming that although Abe’s and Bob’s belief states are represented by the same belief set, this belief set is associated with different selection mechanisms in the two cases. Abe has a selection mechanism that gives priority to \(q\) over \(p \leftrightarrow q\), whereas Bob’s selection mechanism has the opposite priorities.)
There is only one inconsistent belief set (logically closed inconsistent set), namely the whole language. On the other hand there are, in any non-trivial logic, many different inconsistent belief bases. Therefore, belief bases make it possible to distinguish between different inconsistent belief states.
In belief revision theory it has mostly been taken for granted that belief sets correspond to a coherentist epistemology, whereas belief bases represent foundationalism. However, the logical relationships among the elements of a logically closed set do not adequately represent epistemic coherence. Although coherentists typically claim that all beliefs contribute to the justification of other beliefs, they hardly mean this to apply to merely derived beliefs such as “either Paris or Rome is the capital of France”, that one believes only because one believes Paris to be the capital of France. Therefore, the distinction between operations on belief bases and operations on belief sets should not be equated with that between foundationalism and coherentism.
5.2 Belief base contraction
Partial meet contraction, as defined in Section 2.1, is equally applicable to belief bases. Note that \(A\bot p\) is the set of maximal subsets of \(A\) that do not imply \(p\); it is not sufficient that they do not contain \(p\). Hence
\[ \{p, p \amp q, p \vee q, p \leftrightarrow q\} \bot p = \{\{p \vee q\}, \{p \leftrightarrow q\}\}. \]Most of the basic postulates for partial meet contraction on belief sets hold for belief bases as well. However, Recovery does not hold for partial meet contraction of belief bases. This can be seen from the following example (that is adopted from Isaac Levi (2004) who used it for other purposes:
Let the belief set \(K\) include both a belief that the coin was tossed \((c)\) and a belief that it landed heads \((h)\). The epistemic agent wishes to consider whether, on the supposition that the coin had been tossed, it would have landed heads. In order to do that, it would seem reasonable to remove \(c\) from the belief set and then reinsert it, i.e. to perform the series of operations \(K\div c+c\).
(1) If partial meet contraction is performed directly on the belief set, then it follows from Recovery that \(h \in K\div c+c\), i.e. \(h\) comes back with \(c\). This is contrary to reasonable intuitions.
(2) If partial meet contraction is instead performed on a belief base for \(K\), then recovery can be avoided. Let the belief base be \(\{p_1 ,\ldots ,p_n, c, h\}\), where the background beliefs \(p_1 ,\ldots ,p_n\) are unrelated to \(c\) and \(h\), whereas \(h\) logically implies \(c\). Then \(K = \Cn(\{p_1 ,\ldots ,p_n, c, h\})\). Since \(h\) implies \(c\), it will have to go when \(c\) is removed, so that \(K\div c = \Cn(\{p_1 ,\ldots ,p_n\})\). When \(c\) is reinserted, the outcome is \((K\div c)+c = \Cn(\{p_1 ,\ldots ,p_n, c\})\) that does not contain \(h\), as desired.
The following representation theorem has been obtained for partial meet contraction on belief bases (Hansson 1999). An operation \(\div\) is a partial meet contraction for a set \(A\) if and only if it satisfies the following four postulates:
Success:
If \(p \not\in \Cn(\varnothing)\), then \(p \not\in \Cn(A\div
p)\).
Inclusion:
\(A\div p \subseteq A\)
Relevance:
If \(q \in A\) and \(q \not\in A\div p\), then there is a set \(A'\)
such that \(A\div p \subseteq A' \subseteq A\) and that \(p \not\in
\Cn(A')\) but \(p \in \Cn(A'\cup \{q\})\).
Uniformity:
If it holds for all subsets \(A'\) of \(A\) that \(p \in \Cn(A')\) if
and only if \(q \in \Cn(A')\), then \(A\div p = A\div q\).
The Relevance postulate has much the same function as Recovery has for belief sets, namely to prevent unnecessary losses of beliefs.
An alternative approach to contraction of belief bases has been proposed under the name kernel contraction. For any sentence \(p\), a \(p\)-kernel is a minimal \(p\)-implying set, i.e. a set that implies \(p\) but has no proper subset that implies \(p\). A contraction operation \(\div\) can be based on the simple principle that no \(p\)-kernel should be included in \(A\div p\). This can be obtained with an incision function, a function that selects at least one element from each \(p\)-kernel for removal. An operation that removes exactly those elements that are selected for removal by an incision function is called a kernel contraction. It turns out that all partial meet contractions on belief bases are kernel contractions, but some kernel contractions are not partial meet contractions. In other words, kernel contraction is a generalization of partial meet contraction.
5.3 Belief base revision
The operation of expansion for belief sets, \(K+p = \Cn(K\cup \{p\})\), was constructed to ensure that the outcome is logically closed. This is not desirable for belief bases, and therefore expansion on belief bases must be different from expansion on belief sets. For any belief base \(A\) and sentence \(p,\) \(A +' p\), the (non-closing) expansion of \(A\) by \(p\), is the set \(A\cup \{p\}\).
Just like the corresponding operations for belief sets, revision operations for belief bases can be constructed out of two suboperations: expansion by \(p\) and contraction by \(\neg p\). According to the Levi identity, \((A* p = (A\div \neg p) +' p)\), the contractive suboperation should take place first. Alternatively, the two suboperations may take place in reverse order, \(A* p = (A+'p) \div \neg p\). This latter possibility does not exist for belief sets. If \(K\cup \{p\}\) is inconsistent, then \(K+p\) is always the same, namely identical to the whole language, independently of the identity of \(K\) and of \(p\), so that all distinctions are lost. For belief bases, this limitation is not present, and thus there are two distinct ways to obtain revision from contraction and expansion:
Internal revision:
\(A * p = (A \div \neg p) +' p\)
External revision:
\(A * p = (A +' p) \div \neg p\)
Intuitively, external revision by \(p\) is revision with an intermediate inconsistent state in which both \(p\) and \(\neg p\) are believed, whereas internal revision has an intermediate non-committed state in which neither \(p\) nor \(\neg p\) is believed. External and internal revision differ in their logical properties, and neither of them can be subsumed under the other.
5.4 Connections between belief bases and belief sets
A contraction on a belief base gives rise to a contraction on its corresponding belief set. Let \(A\) be a belief base and \(K = \Cn(A)\) its corresponding belief set. Furthermore, let \(-\) be a contraction on \(A\). It gives rise to an operation \(\div\) of base-generated contraction on \(K\), such that for all sentences \(p: K\div p = \Cn(A-p)\). Base-generated contraction has been axiomatically characterized. An operation \(\div\) on a consistent belief set \(K\) is generated by an operation of partial meet contraction for some finite base for \(K\) if and only if it satisfies the following eight postulates:
Closure:
\(K\div p = \Cn(K\div p)\)
Success:
If \(p \not\in \Cn(\varnothing)\), then \(p \not\in \Cn(K\div
p)\).
Inclusion:
\(K\div p \subseteq K\)
Vacuity:
If \(p \not\in \Cn(K)\), then \(K\div p = K\).
Extensionality:
If \(p\leftrightarrow q \in \Cn(\varnothing)\), then \(K\div p = K\div
q\).
Finitude:
There is a finite set \(X\) such that for every sentence \(p\),
\(K\div p = \Cn(X')\) for some \(X' \subseteq X\).
Symmetry:
If it holds for all \(r\) that \(K\div r \vdash p\) if and only if
\(K\div r \vdash q\), then \(K\div p = K\div q\).
Conservativity:
If \(K\div q\) is not a subset of \(K\div p\), then there is some
\(r\) such that \(K\div p \subseteq K\div r \not\vdash p\) and \(K\div
r \cup K\div q \vdash p\).
Operations of revision on a belief set can be base-generated in the same sense as operations of contraction.
6. Other operations
The AGM framework has been extended in many ways. Some of these extensions have introduced new types of operations in addition to the three standard types in AGM, namely contraction, expansion, and revision.
6.1 Update
There are two types of reasons why the epistemic agent may wish to add new information to the belief set. One is that she has received new information about the world, the other that the world has changed. It is common to reserve the term “revision” for the first of these types, and use the term “updating” for the second. The logic of updating differs from that of revision. This can be seen from the following example:
To begin with, the agent knows that there is either a book on the table \((p)\) or a magazine on the table \((q)\), but not both.
Case 1: The agent is told that there is a book on the table. She concludes that there is no magazine on the table. This is revision.
Case 2: The agent is told that after the first information was given, a book has been put on the table. In this case she should not conclude that there is no magazine on the table. This is updating.
One useful approach to updating is to assign time indices to the sentences, as proposed by Katsuno and Mendelzon (1992). Then the belief set will not consist of sentences \(p\) but of pairs \(\langle p,t_1\rangle\) of a sentence \(p\) and a point in time \(t_1\), signifying that \(p\) holds at \(t_1\). In the book-and-magazine example, let \(t_1\) denote the point in time that the first statement refers to, and \(t_2\) the moment when the second information was given in Case 2. The original belief set contained the pair \(\langle \neg(p\leftrightarrow q),t_1\rangle\). (\(\neg(p\leftrightarrow q)\) is the exclusive disjunction of \(p\) and \(q\).) Revision by \(p\) can be represented by the incorporation of \(\langle p,t_1\rangle\), and updating by \(p\) by the incorporation of \(\langle p,t_2\rangle\) into the belief set. It follows quite naturally that \(\langle \neg q,t_1\rangle\) is implied by the revised belief set but not by the updated belief set.
6.2 Consolidation
If a belief base is inconsistent, then it can be made consistent by removing enough of its more dispensable elements. This operation is called consolidation. The consolidation of a belief base \(A\) is denoted \(A!\). A plausible way to perform consolidation is to contract by falsum (contradiction), i.e. \(A! = A\div\smbot\).
Unfortunately, this recipe for consolidation of inconsistent belief bases does not have a plausible counterpart for inconsistent belief sets. The reason is that since belief revision operates within classical logic, there is only one inconsistent belief set. Once an inconsistent belief set has been obtained, all distinctions have been lost, and consolidation cannot restore them.
6.3 Semi-revision
By non-prioritized belief change is meant a process in which new information is received, and weighed against old information, with no special priority assigned to the new information due to its novelty. A (modified) revision operation that operates in this way is called a semi-revision. Semi-revision of \(K\) by a sentence \(p\) can be denoted \(K?p\). A sentence \(p\) that contradicts previous beliefs is accepted only if it has more epistemic value than the original beliefs that contradict it. In that case, enough of the previous sentences are deleted to make the resulting set consistent. Otherwise, the input is itself rejected.
One way to construct semi-revision on a belief base \(A\) is to let it consist of two suboperations:
- Expand \(A\) by \(p\).
- Restore consistency by giving up either \(p\) or some original belief(s).
This amounts to defining semi-revision in terms of expansion and consolidation:
\[ A?p = (A +' p)! \]This identity cannot be used for belief sets. Since all inconsistent belief sets are identical, an operation ? such that \(K?p = (K+p)!\) will have the extremely implausible property that if \(\neg p_1 \in K_1\) and \(\neg p_2 \in K_2\), then \(K_1 ?p_1 = K_2 ?p_2\). However, other ways to perform semirevision on belief sets have been proposed, in particular, the following two-step process:
- Decide whether the input \(p\) should be accepted or rejected.
- If \(p\) was accepted, revise by \(p\).
A simple way to apply this recipe is David Makinson’s (1997) screened revision, in which there is a set \(X\) of potential core beliefs that are immune to revision. The belief set \(K\) should be revised by the input sentence \(p\) if \(p\) is consistent with the set \(X\cap K\) of actual core beliefs, otherwise not. The second step of screened revision is a revision of \(K\) by \(p\), but with the restriction that no element of \(X\cap K\) is allowed to be removed.
Another variant of the same recipe is called credibility-limited revision. It is based on the assumption that some inputs are accepted, others not. Those that are accepted form the set C of credible sentences. If \(p \in\) C, then \(K?p = K* p\). Otherwise, \(K?p = K\). This construction can be further specified by choosing an operation of revision and assigning properties to the set C. A variety of such constructions have been investigated (Hansson et al. 2001).
6.4 Selective revision
Selective revision is a generalization of semi-revision. In semi-revision, the input information is either rejected or fully accepted. In selective revision, it is possible for only a part of the input information to be accepted. An operation \(\circ\) of selective revision can be constructed from a standard revision operation \(*\) and a transformation function \(f\) from and to sentences:
\[ K \circ p = K * f(p) \]In the intended cases, \(f(p)\) does not contain any information that is not contained in \(p\). This is ensured if \(f(p)\) is a logical consequence of \(p\). By adding further conditions on \(f\), various additional properties can be obtained for the operation of selective revision.
6.5 Shielded contraction
The Success postulate of contraction requires that all non-tautological beliefs are retractable. This is not a fully realistic requirement, since actual agents are known to have beliefs of a non-logical nature that nothing can bring them to give up. In shielded contraction, some non-tautological beliefs cannot be given up; they are shielded from contraction. Shielded contraction can be based on an ordinary contraction \(\div\) and a set \(R\) of retractable sentences. If \(p \in R\), then \(K-p = K\div p\). Otherwise, \(K-p = K\).
This construction can be further specified by adding various requirements on the structure of \(R\). Close connections have been shown to hold between shielded contraction and semi-revision. (Fermé and Hansson 2001)
6.6 Replacement
By replacement is meant an operation that replaces one sentence by another in a belief set. It is an operation with two variables, such that \([p/q]\) replaces \(p\) by \(q\). Hence, \(K[p/q]\) is a belief set that contains \(q\) but not \(p\).
Replacement aims both at the removal of a sentence \(p\) and the addition of a sentence \(q\). This amounts to two success conditions, \(p \not\in K[p/q]\) and \(q \in K[p/q]\). However, these two conditions cannot both be satisfied without exception. First, just as for belief contraction, an exception must be made from the first of them in the case when \(p\) is a tautology and so cannot be removed. Secondly, the two conditions are not compatible in cases when \(q\) logically implies \(p\). This can be dealt with by extending the exception that is provided for in the Success postulate for contraction from cases when \(p \in \Cn(\varnothing)\) to cases when \(p \in \Cn(\{q\})\). This gives rise to the following two success conditions:
Contractive success:
If \(p \not\in \Cn(\{q\})\), then \(p \not\in \Cn(K[p/q]\)).
Revision success:
\(q \in K[p/q]\)
Replacement can be used as a kind of “Sheffer stroke” for belief revision, i.e. as an operation in terms of which the other operations can be defined. Contraction by \(p\) can be defined as \(K[p/\smtop]\) and revision by \(p\) as \(K[\smbot/p]\), where \(\smbot\) is falsum and \(\smtop\) is tautology. Provided that the unperformable suboperation of removing the tautology \(\smtop\) is treated as an empty suboperation, expansion by \(p\) can be defined as \(K[\smtop/p]\).
6.7 Merge
If the belief set \(K\) has a finite base, then it can be represented by a single sentence, namely the conjunction \(k\) of all the elements of its base. This means that the revision \(K* p\) of a belief set \(K\) by a sentence \(p\) can be replaced by a revision \(k* p\) of a sentence by another sentence. If this revision is non-prioritized, we may treat \(k\) and \(p\) equally, so that \(k* p = p* k\). Such an operation can be described as the merging of two belief representations. It can represent a process of conflict resolution through selective combination of information from two agents or sources. This operation can also be generalized to the merge of several elements, representing efforts to combine information from several agents or sources (Konieczny and Pino Pérez 2011).
6.8 Multiple contraction and revision
By multiple contraction is meant the simultaneous contraction of more than one sentence. Similarly, multiple revision is revision by more than one sentence.
There are two major types of multiple contraction. In package contraction, all elements of the input set are retracted: they have to go in a package. In choice contraction it suffices to remove at least one of them. Hence, the success conditions for the two types of multiple contraction are as follows:
Package success:
If \(B\cap \Cn(\varnothing) = \varnothing\) then \(B\cap \Cn(A\div B)
= \varnothing\)
Choice success:
If \(B\) is not a subset of \(\Cn(\varnothing)\), then \(B\) is not a
subset of \(\Cn(A\div B)\).
Partial meet contraction and kernel contraction can both be generalized fairly straight-forwardly to both package and choice variants of multiple contraction.
The construction of package revision gives rise to an interesting extension of the notion of negation. The reason why contraction by \(\neg p\) is performed as a suboperation of revision by \(p\) is that \(p\) can be consistently added to a set if and only if it does not imply \(\neg p\). It turns out that (in a logic satisfying compactness) a set \(B\) can be consistently added to another set if and only if this other set does not imply any element of the set \(\neg B\), that is defined as follows:
Negation of a set:
\(p \in \neg B\) if and only if \(p\) is either a negation of an
element of \(B\cup \{\smtop\}\) or a disjunction of negations of
elements of \(B\cup \{\smtop\}\).
Therefore multiple revision can be defined from (package) multiple contraction and expansion via a generalized Levi identity:
\[ K* B = (K\div \neg B)+B \]Most of the major AGM-related contraction operations have been generalized to multiple contraction: multiple partial meet contraction (Hansson 1989, Fuhrmann and Hansson 1994, Li 1998), multiple kernel contraction (Fermé et al. 2003), multiple specified meet contraction (Hansson 2010), and a multiple version of Grove’s sphere system (Reis and Fermé 2011, Fermé and Reis 2012).
6.9 Indeterministic belief change
Most models of belief change are deterministic in the sense that given a belief set and an input, the resulting belief set is well-determined. There is no scope for chance in selecting the new belief set. Clearly, this is not a realistic feature, but it makes the models much simpler and easier to handle, not least from a computational point of view. In indeterministic belief change, the subjection of a specified belief set to a specified input has more than one admissible outcome.
Indeterministic operations can be constructed as sets of deterministic operations. Hence, given three revision operations \(* , * '\) and \(* ''\) the set \(\{*\), \(* '\), \(* ''\)\(\}\) can be used as an indeterministic operation. The success condition is simply:
\[ K\{* , * ', * ''\}p \in \{K* p, K* 'p, K* ''p\} \]Lindström and Rabinowicz (1991) constructed indeterministic contraction by giving up the assumption that epistemic entrenchment satisfies connectedness. This resulted in Grove’s sphere systems with “fallbacks” that are not linearly ordered but still all include the original belief set. Fazio and Baldi (2021) have used indeterministic contraction in an investigation of algebraic counterparts to both the AGM model and some closely related models of belief change.
6.10 Operations for an extended language
Belief revision theory has been almost exclusively developed within the framework of classical sentential (truth-functional) logic. The inclusion of non-truthfunctional expressions into the language has interesting and indeed drastic effects. In particular, this applies to conditional sentences.
Many types of conditional sentences, such as counterfactual conditionals, cannot be adequately expressed with truth-functional implication (material implication). Several formal interpretations of conditional sentences have been proposed. One of them, namely the Ramsey test, is particularly well suited to the formal framework of belief revision. It is based on a suggestion by F. P. Ramsey that has been further developed by Robert Stalnaker and others (Stalnaker 1968). The basic idea is that “if \(p\) then \(q\)” is taken to be believed if and only if \(q\) would be believed after revising the present belief state by \(p\). Let \(p\Rightarrow q\) denote “if \(p\) then \(q\)”, or more precisely: “if \(p\) were the case, then \(q\) would be the case”. In order to treat conditional statements on par with statements about actual facts, they will have to be included in the belief set, thus:
The Ramsey test:
\((p\Rightarrow q) \in K\) if and only if \(q \in K* p\).
However, inclusion in the belief set of conditionals that satisfy the Ramsey test will require radical changes in the logic of belief change. As one example of this, contraction cannot then satisfy the inclusion postulate \((K\div p \subseteq K)\). The reason for this is that contraction typically provides support for conditional sentences that were not supported by the original belief state. This can be seen from the following example:
If I give up my belief that John is mentally retarded, then I gain support for the conditional sentence “If John has lived 30 years in London, then John understands the English language.”
A famous impossibility theorem by Peter Gärdenfors (1986, 1987) shows that the Ramsey test is incompatible with a set of plausible postulates for revision. Several solutions to the impossibility theorem have been put forward. One option is to reject the Ramsey test as a criterion for the validity of conditional sentences (Rott 1986). Another, proposed by Isaac Levi, is to accept the test as a criterion of validity but deny that such conditional sentences should be included in the belief set when they are valid (Levi 1988. Arló-Costa 1995. Arló-Costa and Levi 1996). Several other proposals have been put forward. However, it is fair to say that operations of AGM-style belief change have not yet been constructed that are generally recognized as able to deal adequately with conditional or modal sentences.
6.11 Resource-bounded belief change
The AGM model and most related models of belief change assume highly idealized reasoners who have unlimited cognitive capacities. Harman (1986) developed a set of rationality principles for resource-bounded epistemic agents. Wassermann (1999), Alechina (2006), Doyle (2013) and others have developed models of belief change for agents with limited cognitive capacities. The use of finite belief bases (section 5) can be seen as a way to avoid the operations on infinite belief sets that are standard in AGM. Operations on infinite sets can require infinite resources, which makes such operations impossible for agents with finite resources.
6.12 Changes in the strength of beliefs
An operation of change can raise or lower the position of a sentence in the ordering without affecting the belief set (but affecting how the belief state responds to new inputs). An operation of improvement, as proposed by Konieczny and Pérez (2008) increases the plausibility of a non-believed sentence \(p\) by moving some of the \(p\)-worlds to a higher position in the preference ordering of worlds. Even if such a change does not lead to \(p\) becoming a belief, its acceptance in later, additional operations can be facilitated.
An operation of change can be so constructed that it adjusts the position of the input sentence in an ordering to be the same as that of a reference sentence. This means that two sentences have to be specified in the input: the (input) sentence to be moved and the (reference) sentence indicating its new position. Hans Rott (2007, Other Internet Resources) called such operators two-dimensional. John Cantwell (1997) classified them as raising or lowering, depending on the direction of change. (See also Fermé and Rott 2004 and Rott 2009.)
6.13 Changes in norms and preferences
There are close parallels between changes in norms and changes in beliefs. In order to apply a norm system with conflicting norms to a particular situation, some of the norms may have to be ignored. The problem how to prioritize among conflicting norms is similar to the selection of sentences for removal in belief contraction (Hansson and Makinson 1997). The AGM model was in fact partly the outcome of attempts to formalize changes in norms rather than beliefs (Alchourrón and Makinson 1981). In spite of this, authors who apply the AGM model to norms have found it in need of rather extensive modifications to make it suitable for that purpose. Hence, in their model of changes in legislation, Governatori and Rotolo (2010) introduced an explicit representation of time in order to account for phenomena such as retroactivity.
A model of changes in preferences can be obtained by replacing the standard AGM language by sentences of the form \(p \ge q\) (“\(p\) is at least as good as \(q\)”) and their truth-functional combinations. The adoption of a new preference can then take the form of revision by such a preference sentence. Partial meet contraction can be used, but some modifications of the AGM model seem to be necessary in applications to preferences (Hansson 1995, Lang and van der Torre 2008, Grüne-Yanoff and Hansson 2009).
7. Iterated change
The preceding sections have only dealt with changes of one and the same belief set or belief base. This is clearly a severe limitation. A realistic model of belief change should allow for repeated (iterated) changes, such as \(K\div p\div q* r* s\div t\ldots\) In other words, operations are needed that can contract or revise any belief set (belief base) by any sentence. Such operations are called global, in contrast to local operations that are defined only for a single specified set.
An obvious way to obtain a global operation of partial meet contraction would be to use the same selection function for all sets to be contracted. However, with the standard way to obtain a partial meet contraction from a selection function, this is not possible, due to the way selection functions treat the empty set. The way selection functions have traditionally been defined, if \(A\bot p = \varnothing\), then \(\gamma(A\bot p ) = \{A\}\). As a consequence of this, if \(\gamma\) is a selection function for \(A\), and \(A \ne B\), then \(\gamma\) is not a selection function for \(B\). For let \(A\bot p = B\bot p = \varnothing\). For \(\gamma\) to be a function it must be the case that \(\gamma(A\bot p) = \gamma(B\bot p)\). For \(\gamma\) to be a selection function for \(A\) it must be case that \(\gamma(A\bot p) = \{A\}\), and in order for it to be a selection function for \(B\) it must be the case that \(\gamma(B\bot p) = \{B\}\). Since \(A \ne B\), this is impossible.
This can be solved if we rewrite the definition of partial meet contraction as follows:
Alternative definition of partial meet contraction:
\((1')\) \(\gamma(K\bot p) \subseteq K\bot p\), and if \(K\bot p \ne \varnothing\), then \(\gamma(K\bot p) \ne \varnothing\).
\((2')\) \(K\div p = \bigcap \gamma(K\bot p)\), unless \(\gamma(K\bot p) = \varnothing\), in which case \(K\div p = K\).
As applied to a single belief set \(K\), this definition is equivalent with the original definition. Notably, it yields the same result as the original definition even in the limiting case when \(p\) is a tautology, but it avoids using the selection function in this limiting case. With this, slightly adjusted, definition, one and the same selection function can be used for all belief sets, and consequently we can construct iterated change using only one, AGM-style, selection function. Since partial meet revision is definable from partial meet contraction via the Levi identity, this means that we have global operations for both contraction and revision. This construction is so general that it does not impose any new properties on contraction or revision, i.e. no properties in addition to the usual AGM postulates (Hansson 2012).
However, most of the discussion on iterated change has been based on the assumption that such additional properties are plausible and indeed desirable. The so-called Darwiche-Pearl postulates for revision have had a central role in these discussions (Darwiche and Pearl 1997):
If \(q \vdash p\), then \((K * p) * q = K * q\). (DP1)
If \(q \vdash \neg p\), then \((K * p) * q = K * q\). (DP2)
If \(K * q \vdash p\), then \((K * p) * q \vdash p\). (DP3)
If \(K * q\) ⊬ \(\neg p\), then \((K * p) * q\) ⊬ \(\neg p\) (DP4)
The Darwiche-Pearl postulates express an intuition about the epistemic ordering of possible worlds, namely that when we revise by a sentence \(p\), then the ordering among \(p\)-worlds should be unchanged, and so should the ordering among \(\neg p\)-worlds. The change takes the form of a shift of the relative positions of these two parts of the original ordering of worlds. A large number of proposals for such shifts have been put forward, but opinions differ widely on the adequacy of these proposals.
Abhaya Nayak (1994) has proposed a model of iterated belief change in which both the belief states and the inputs are binary relations that satisfy the standard entrenchment postulates except Minimality. Inputs of this type may be seen as “fragments” of belief states, to be incorporated into the previous belief state. In the same vein, Eduardo Fermé and Hans Rott (2004) have investigated belief revision with inputs of the more general form: “accept \(q\) with a degree of plausibility that at least equals that of \(p\)”. They call this revision by comparison. Belief states are represented by entrenchment orderings. Hence, from an entrenchment ordering \(\le\) and such a generalized input a new entrenchment ordering \(\le '\) is obtained that contains the information needed to construct the new belief set.
8. Alternative accounts
In spite of the dominant position of the AGM model and its close variants, several other formal models of belief changes have been proposed.
8.1 Learning theory
In belief revision theory, the focus is on consistency rather than truthfulness. In contrast, learning theory is devoted to induction and the attainment of true beliefs. A research question is represented as a partition of the set of possible worlds, i.e. a distribution of all possible worlds into non-overlapping sets. The research question has been fully answered when it is known which of these partitions contains the actual world. Information received by the agent successively narrows down the set of partitions that may contain it. The central issue is how to construct an inductive strategy, i.e. a strategy for which investigations to perform and in what order, and how to interpret them (Kelly 1999). Although this problem has connections with belief revision, operations not satisfying the standard AGM postulates have usually played a prominent role in the discussion. (Genin and Kelly 2019)
8.2 Dynamic logics of belief change
Dynamic doxastic logic (DDL) was introduced by Krister Segerberg to represent an agent who has opinions about the external world and changes these opinions upon receipt of new information. DDL makes use of epistemic modal operators of the type introduced by Hintikka (1962). The sentence \(B_i p\) denotes that the individual \(i\) believes that \(p\). When only one agent is under consideration, the subscript can be deleted, and the operator \(B\) can be read “it is believed that” or “the agent believes that” (Segerberg 1995, p. 536).
The formula \(Bp\) in DDL differs from the expression \(p \in K\) of AGM in being a sentence in the same language as \(p\). This makes it possible to express in the object language that a sentence is believed. In this way, Segerberg attempted to develop belief revision “as a generalization of ordinary Hintikka type doxastic logic”, whereas in contrast “AGM is not really logic; it is a theory about theories” (Segerberg 1999, p. 136). In the DDL framework it is possible to express beliefs about beliefs. The sentence “\(i\) believes that \(i\) does not believe that \(p\)” can be expressed as \(B_i \neg B_i p\), whereas there is no way to express it in the AGM framework. \(((p \not\in K_i) \in K_i\) is not a well-formed formula.)
In DDL, belief revision operations (expansion, revision, and contraction) are expressed with dynamic modal operators, similar to those used for program execution. (This element of DDL was present also in previous publications by several authors. See Fuhrmann 1991; de Rijke 1994; van Benthem 1989 and 1995.) Segerberg used the following notation:
| \([\div p]q\) | (\(q\) holds after contraction by \(p)\) |
| \([* p]q\) | (\(q\) holds after revision by \(p)\) |
| \([+ p]q\) | (\(q\) holds after expansion by \(p)\) |
The combination of these two elements, belief operators and dynamic operators, results in a framework that differs from AGM in important ways. (Leitgeb and Segerberg 2007, 169)
Largely similar systems have been developed under the name of Dynamic Epistemic Logic, DEL (Plaza 1989; Baltag et al. 1998; van Ditmarsch et al. 2007; see the entry on dynamic-epistemic logic). A major difference between DDL and DEL is that the latter has mostly been studied in multiagent contexts. The most studied dynamics is that of the public announcement of some sentence (van Ditmarsch et al. 2007).
8.3 Descriptor revision
Descriptor revision (Hansson 2017) is based on two major formal constructions. One of them is a metalinguistic belief predicate \(\mathfrak{B}\) that is applied to sentences of the object language. \(\mathfrak{B}p\) denotes that the sentence \(p\) is believed, \(\neg \mathfrak{B}p\) that it is not believed, and \(\mathfrak{B}p\vee \mathfrak{B}q\) that either \(p\) or \(q\) is believed. Such sentences can be used to express the success conditions of belief change operations. Thus \(\mathfrak{B}p\) is the success condition of revision by \(p\), \(\neg \mathfrak{B}p\) that of contraction by \(p\) and \(\{\neg \mathfrak{B}p,\neg \mathfrak{B}q\}\) that of multiple contraction by \(\{p,q\}\). Due to the versatility of descriptors we only need one operation, denoted \(\circ\). Hence, \(K\circ \mathfrak{B}p\) represents revision by \(p\) and \(K \circ \neg \mathfrak{B}p\) contraction by \(p\).
The other major formal construction is a choice function (selection function) that operates directly on the set of potential outcomes of an operation. Hence, the operation \(K \circ \mathfrak{B}p\) is performed by choosing one among the potential belief sets that contain \(p\) (presumably that which is most choiceworthy, or closest at hand). Operations based on these principles have been axiomatically characterized. Notably, the recovery postulate that creates problems in the AGM framework does not hold in the descriptor revision framework. The application of a choice function to potential belief outcomes is arguably more plausible than its application to possible worlds or remainders, since the latter two entities are logically infinite (if the language is so), and therefore cognitively inaccessible.
Descriptor revision makes it possible to investigate operations of change more generally, and to discuss properties that can hold for operations with different types of the success conditions. Let \( \Psi\) and \( \Xi\) be descriptors, i.e. sets of sentences containing the \( \mathfrak{B}\) operator. Let \(K ⊩\Psi\) denote that \(K\) satisfies all the conditions in \(\Psi\). Some examples of such general properties of descriptor revision are:
Closure:
\(K \circ \Psi = \Cn(K \circ \Psi)\)
Relative success:
\(K \circ \Psi ⊩ \Psi\) or \( K \circ \Psi=K\)
Regularity:
If \(K \circ \Xi ⊩ \Psi\), then \(K \circ \Psi ⊩
\Psi\)
Confirmation:
If \(K ⊩\Psi\), then \(K \circ \Psi=K)\)
Cumulativity:
If \(K \circ \Psi ⊩\Xi\), then \(K \circ \Psi = K \circ
(\Psi\cup\Xi) \)
8.4 Bayesian models
The AGM model and other logical frameworks for belief revision are based on a dichotomous approach to belief: either something is believed or it is not, in either case without any gradations. Beliefs can be be more or less easily given up, and non-beliefs can be more or less easily turned into beliefs, but the very act of believing does not admit of degrees. In contrast, probabilistic models of belief, usually based on some form of subjective Bayesianism, admit all degrees between the strongest belief and the strongest disbelief. Dichotomous and probabilistic models represent different features of belief systems. It has proved to be difficult to construct a reasonably manageable model that covers both the logic-related and the probabilistic properties of belief change. These difficulties are closely connected with the lottery and preface paradoxes (Kyburg 1961; Makinson 1965).
However, belief revision theory has turned out to be useful in dealing with the problematic limiting case of conditional probabilities with a condition that has probability zero. Insights from belief revision theory have been used in the construction of non-standard models of probabilities in which conditionalization can be performed also in this limiting case (Makinson 2011).
Bibliography
Citations annotated in smaller text refer to books or articles that are recommended for further introductory reading.
- Alchourrón, C.E., P. Gärdenfors, and D. Makinson,
1985, “On the Logic of Theory Change: Partial Meet Contraction
and Revision Functions”, Journal of Symbolic Logic, 50:
510–530.
[The starting-point for all subsequent studies of belief revision.] - Alchourrón, C.E. and D. Makinson, 1981, “Hierarchies of Regulation and Their Logic”, in R. Hilpinen (ed.), New Studies in Deontic Logic, Dordrecht: D. Reidel Publishing Company, pp. 125–148.
- Alchourrón, C.E. and D. Makinson, 1982, “On the logic of theory change: Contraction functions and their associated revision functions”, Theoria, 48: 14–37.
- Alechina, N., M. Jago, and B. Logan, 2006, “Resource-bounded belief revision and contraction”, Lecture Notes in Computer Science, 3904: 141–154.
- Arló-Costa, H., 1995, “Epistemic conditionals, snakes and stars”, in G. Crocco, L. Fariñas del Cerro, and A. Herzig (eds.), Conditionals: from Philosophy to Computer Science, Studies in Logic and Computation (Volume 5), Oxford: Oxford University Press.
- Arló-Costa, H. and I. Levi, 1996, “Two notions of epistemic validity”, Synthese, 109: 217–262.
- Baltag, A., Moss, L., and Solecki, S., 1998, “The logic of public announcements, common knowledge, and private suspicions”, in I. Gilboa (ed.), Proceedings of the 7th conference on theoretical aspects of rationality and knowledge (TARK ’98), San Francisco: Morgan Kaufmann, pp. 43–56.
- Berto, F., 2019, “Simple hyperintensional belief revision”, Erkenntnis, 84: 559–575.
- Cantwell, J., 1997, “On the logic of small changes in hypertheories”, Theoria, 63: 54–89.
- –––, 1999, “Some logics of iterated
revision”, Studia Logica, 7: 49–84.
[Iterated revision.] - Darwiche, A. and J. Pearl, 1997, “On the logic of iterated belief revision”, Artificial Intelligence, 89: 1–29.
- de Rijke, M., 1994, “Meeting some neighbours”, in J. van Eijck, and A. Visser (eds.) Logic and information flow, Cambridge, MA: MIT Press, pp. 170–195.
- Doyle, J., 1979, “A Truth Maintenance System”, Artificial Intelligence, 12: 231–272.
- –––, 2013, “Mechanics and mental change”. In B.O. Küppers et al. (eds) Evolution of Semantic Systems, pp. 127–150. Springer: Cham.
- Fagin, R., J.D. Ullman, and M.Y. Vardi, 1983, “On the semantics of updates in databases”, Proceedings of Second ACM SIGACT-SIGMOD, pp. 352-365.
- Fazio, D. and M. Pra Baldi, 2021, “On a logico-algebraic approach to AGM belief contraction theory”, Journal of Philosophical Logic, 50: 911–938.
- Fermé, E. and S.O. Hansson, 2001, “Shielded Contraction”, pp. 85–107 in H. Rott and M.-A. Williams (eds.), Frontiers of Belief Revision, Dordrecht: Kluwer.
- –––, 2018, Belief Change. Introduction and
Overview, Springer: Cham.
[Overview of results from studies of belief revision in the AGM tradition and related approaches.] - Fermé, E. and M.D.L. Reis, 2012, “System of Spheres-based Multiple Contractions”, Journal of Philosophical Logic, 41: 29–52.
- Fermé, E. and H. Rott, 2004, “Revision by comparison”, Artificial Intelligence, 157: 5–47.
- Fermé, E., K. Saez, and P. Sanz, 2003, “Multiple Kernel Contraction”, Studia Logica, 73: 183–195.
- Fuhrmann, A., 1991, “Theory contraction through base contraction”, Journal of Philosophical Logic, 20: 175–203.
- Fuhrmann, A. and S.O. Hansson, 1994, “A Survey of Multiple
Contraction”, Journal of Logic, Language and
Information, 3: 39–74.
[Multiple contraction] - Gärdenfors, P., 1978, “Conditionals and Changes of Belief”, Acta Philosophica Fennica, 30: 381–404.
- –––, 1981, “An Epistemic Approach to Conditionals”, American Philosophical Quarterly, 18: 203–211.
- –––, 1986, “Belief Revision and the Ramsey
Test for Conditionals”, Philosophical Review, 95:
81–93.
[The Ramsey Test.] - –––, 1987, “Variations on the Ramsey Test: More triviality results”, Studia Logica, 46: 319–325.
- –––, 1988, Knowledge in Flux. Modeling the
Dynamics of Epistemic States, Cambridge, MA: MIT Press.
[The AGM model.] - –––, 2011, “Notes on the history of ideas behind AGM”, Journal of Philosophical Logic, 40: 115–120.
- Gärdenfors, P., and D. Makinson, 1988, “Revisions of Knowledge Systems Using Epistemic Entrenchment”, Second Conference on Theoretical Aspects of Reasoning about Knowledge, pp. 83–95.
- Genin, K. and K.T. Kelly, 2019,“Theory Choice, Theory Change, and Inductive Truth-Conduciveness”, Studia Logica, 107: 949–989.
- Governatori, G. and A. Rotolo, 2010, “Changing legal systems: legal abrogations and annulments in Defeasible Logic”, Logic Journal of IGPL, 18: 157–194.
- Grove, A., 1988, “Two Modellings for Theory Change”,
Journal of Philosophical Logic, 17: 157–170.
[The propositional model of belief change.] - Grüne-Yanoff, T. and S.O. Hansson, 2009, “From Belief Revision to Preference Change”, in T. Grüne-Yanoff and S.O. Hansson (eds.), Preference Change: Approaches from Philosophy, Economics and Psychology, Berlin: Springer, pp. 159–184.
- Hansson, S.O., 1989, “New Operators for Theory Change”, Theoria, 55: 114–132.
- –––, 1995, “Changes in Preference”, Theory and Decision, 38: 1–28.
- –––, 1999, A Textbook of Belief Dynamics.
Theory Change and Database Updating, Dordrecht: Kluwer.
[Contains more details, and references, on most of the topics treated in this entry.] - –––, 2003, “Ten Philosophical Problems in
Belief Revision”, Journal of Logic and Computation, 13:
37–49.
[Connections between belief revision and issues in informal philosophy.] - –––, 2010, “Multiple and Iterated Contraction Reduced to Single-Step Single-Sentence Contraction”, Synthese, 173: 153–177.
- –––, 2012, “Global and iterated contraction and revision: An exploration of uniform and semi-uniform approaches”, Journal of Philosophical Logic, 41(1): 143–172.
- –––, 2017, Descriptor Revision Springer: Cham. Dordrecht: Springer.
- Hansson, S.O., Fermé, E., Cantwell, J., and Falappa, M.,
2001, “Credibility-Limited Revision”, Journal of
Symbolic Logic, 66: 1581–1596.
[Non-prioritized belief revision.] - Hansson, S.O. and D. Makinson, 1997, “Applying Normative rules with restraint”, in M.L. Dalla Chiara, et al. (eds.), Logic and Scientific Method, Dordrecht: Kluwer Academic Publishers, pp 313–332.
- Harman, G., 1986, Change in View – Principles of Reasoning. MIT Press.
- Harper, W., 1977, “Rational Conceptual Change”, PSA 1976, pp. 462–494.
- Hintikka, J., 1962, Knowledge and belief: An introduction to the logic of the two notions, Ithaca: Cornell University Press.
- Katsuno, H., and A.O. Mendelzon, 1992, “On the Difference between Updating a Knowledge Base and Revising it”, in P. Gärdenfors (ed.), Belief Revision, Cambridge: Cambridge University Press pp. 183–203
- Kelly, K.T., 1999, “Iterated belief revision, reliability, and inductive amnesia”, Erkenntnis, 50(1): 7–53.
- Konieczny, S. and R. P. Pérez, 2008, “Improvement Operators”, Eleventh International Conference on Principles of Knowledge Representation and Reasoning (KR08), pp. 177–186.
- –––, 2011, “Logic based merging”, Journal of Philosophical Logic, 40(2): 239–270.
- Kyburg Jr, H.E., 1961, Probability and the logic of rational belief, Middletown: Wesleyan University Press.
- Lang, J. and L. van der Torre, 2008, “From Belief Change to Preference Change”, in M. Ghallab, C.D. Spyropoulos, N. Fakotakis, and N.M. Avouris (eds.), ECAI 2008 – Proceedings of the 18th European Conference on Artificial Intelligence, Patras, Greece, July 21–25, 2008 (Frontiers in Artificial Intelligence and Applications: Volume 178), pp. 351–355.
- Leitgeb, H. and Segerberg, K., 2007, “Dynamic doxastic logic: why, how, and where to?”, Synthese, 155: 167–190.
- Levi, I., 1977, “Subjunctives, Dispositions and Chances”, Synthese, 34: 423–455.
- –––, 1980, The Enterprise of Knowledge, Cambridge, MA: MIT Press.
- –––, 1988, “Iteration of conditionals and the Ramsey test”, Synthese, 76: 49–81.
- –––, 1991, The Fixation of Belief and Its Undoing, Cambridge, MA: Cambridge University Press.
- –––, 2004, Mild Contraction. Evaluating Loss of Information due to Loss of Belief, Oxford: Clarendon Press.
- Li, J., 1998, “A Note on Partial Meet Package Contraction”, Journal of Logic, Language and Information, 7: 139–142.
- Lindström, S. and W. Rabinowicz, 1991, “Epistemic entrenchment with incomparabilities and relational belief revision”, in A. Fuhrmann and M. Morreau (eds.), The Logic of Theory Change, Berlin: Springer, pp. 93–126.
- Makinson, D., 1965, “The paradox of the preface”, Analysis, 25(6): 205–207.
- –––, 1997, “Screened Revision”, Theoria, 63 (1–2): 14–23.
- –––, 2003, “Ways of doing logic: what was new about AGM 1985”, Journal of Logic and Computation, 13: 5–15.
- –––, 2011, “Conditional probability in the light of qualitative belief change”, Journal of Philosophical Logic, 40(2): 121–153.
- Nayak, A. C., 1994, “Iterated Belief Change Based on Epistemic Entrenchment”, Erkenntnis, 41: 353–390.
- Plaza, J., 1989, “Logics of public communications”, in M.L. Emrich, M.S. Pfeifer, M. Hadzikadic, and Z.W. Ras (eds.) Proceedings of the 4th international symposium on methodologies for intelligent systems, Oak Ridge, TN: Oak Ridge National Laboratory, pp. 201–216.
- Reis, M.D.L. and E. Fermé, 2012, “Possible Worlds Semantics for Partial Meet Multiple Contraction”, Journal of Philosophical Logic, 41: 7–28.
- Rott, H., 1986, “Ifs, though and because”, Erkenntnis, 25: 345–37.
- –––, 2001, Change, choice and inference. A
study of belief revision and nonmonotonic reasoning, Oxford:
Clarendon Press.
[The relation between belief change and rational choice.] - –––, 2009, “Shifting Priorities: Simple Representations for Twenty-seven Iterated Theory Change Operators”, in D. Makinson, J. Malinowski and H. Wansing (eds.), Towards Mathematical Philosophy (Trends in Logic: Volume 28), Berlin: Springer, pp. 269–296.
- Rott, H. and M. Pagnucco, 2000, “Severe Withdrawal (and Recovery)”, Journal of Philosophical Logic, 29: 501–547.
- Segerberg, K., 1995, “Belief revision from the point of view of doxastic logic”, Logic Journal of the IGPL, 3: 535–553.
- –––, 1999, “Two traditions in the logic of belief: bringing them together”, in H.J. Ohlbach and U. Reyle (eds.), Logic, Language and Reasoning: essays in honour of Dov Gabbay, Dordrecht: Kluwer Academic Publishers, pp. 135–147.
- Stalnaker, R., 1968, “A Theory of Conditionals”, in N. Rescher (ed.), Studies in Logical Theory, Oxford: Blackwell, pp. 98–112.
- van Benthem, J., 1989, “Semantic Parallels in Natural Language and Computation”, in H.-D. Ebbinghaus, J. Fernandez-Prida, M. Garrido, D. Lascar, and M. Rodrigues Artalejo (eds.), Logic Colloquium ’87, Amsterdam: North-Holland, pp. 331–375.
- –––, 1995, “Logic and the flow of information”, in Proceedings of the 9th international congress of logic, methodology and philosophy of science, Studies in Logic and the Foundations of Mathematics, 134: 693–724.
- van Ditmarsch, H., W. van Der Hoek, and B. Kooi, 2007, Dynamic Epistemic Logic, Dordrecht: Springer.
- Wassermann, R., 1999, “Resource bounded belief revision”, Erkenntnis, 50: 429–446.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
- Rott, H., 2007, “Bounded Revision: Two Dimensional Belief Change Between Conservative and Moderate Revision”, in T. Rønnow-Rasmussen, B. Petersson, J. Josefsson and D. Egonsson, Hommage à Wlodek, Philosophical Papers Dedicated to Wlodek Rabinowicz.


