William of Sherwood
William of Sherwood (Guilelmus, Willelmus, Schyrwode, Shirwode, Shyreswode, and others) was a 13th century English logician who taught at the University of Paris and who worked in the Realist tradition of logic. His Introduction to Logic, written in the middle of the century, was one of the four most influential textbooks on logics in the 13th century, along with Lambert of Auxerre’s Summary, Roger Bacon’s Art and Science of Logic, and Peter of Spain’s Summaries of Logic. Roger Bacon in his Opus tertium (1267) singles Sherwood out for high praise, describing him as “much wiser than Albert [the Great]; for in philosophia communis no one is greater than he” (Kretzmann 1966, pp. 5–6; Kretzmann 1968, pp. 3–4).
- 1. Life and works
- 2. Important doctrines
- 3. Influence
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Life and works
William of Sherwood was born between 1200 and 1205, probably in Nottinghamshire, and died between 1266 and 1272. His school career is uncertain, but given references to his works and his influence on people such as Peter of Spain, Lambert of Auxerre, Albert the Great, and Thomas Aquinas, it is likely that he was teaching logic at the University of Paris between 1235 and 1250. After that period, he seems to have left logic. He was a master at Oxford in 1252 and treasurer of the cathedral of Lincoln about two years later; still later, he was rector at Aylesbury, in Buckinghamshire, and Attleborough, in Norfolk. He was still alive in 1266 but dead by 1272 (Kretzmann 1968, p. 3).
Part of the difficulty with establishing his biography is that he has previously been conflated with various other 13th-century Englishmen named William, such as William of Leicester (d. 1213) and William of Durham (d. 1249) (cf. Grabmann 1937, pp. 11–13; Kretzmann 1966, p. 3; Mullinger 1873, p. 177). He has also sometimes been identified with others bearing the same surname, such as the author of commentary, now lost, on the Sentences of Peter Lombard with the title Shirovodus super sententias, a work that was known to John Leland in the 16th century (Kretzmann 1966, p. 12), or Ricardus de Schirewode, who wrote a treatise on insolubles surviving in Cambridge, St John’s MS 100. This confusion, along with the usual problems presented by anonymous material, makes it difficult to identify William’s works with certainty.
Two works can be confidently ascribed to Sherwood, an Introduction to Logic and a treatise on syncategorematic terms, the Syncategoremata. The Introduction survives in complete form in only one manuscript, Bibliothèque Nationale MS. Lat. 16,617, from the late 13th or 14th century, which begins with the heading Introductiones Magistri Guilli. de Shyreswode in logicam, “Introduction to Logic of Master William of Sherwood”. The Syncategoremata immediately follows, and is likewise explicitly attributed to Sherwood. The Syncategoremata also survives in a second manuscript, Bodleian MS Digby 55, where it is again explicitly labeled, Sincategoreumata Magistri Willielmi de Sirewode “[Treatise on] Syncategorematics of Master William of Sherwood”, and Chapter Five of the Introduction survives in a second manuscript, MS Worcester Cath. Q. 13, written around 1293/94, and edited by Pinborg & Ebbesen (1984).
The Introduction was almost certainly written while William was lecturing on logic at the University of Paris. It was first edited by Grabmann (1937) and translated into English by Kretzmann (1966). A new critical edition was produced by Brands and Kann (1995), accompanied by a translation into German. It has been argued (Mullinger 1873, p. 177) that this book was heavily influenced by a Synopsis treatise written by the 11th-century Byzantine logician Michael Constantine Psellus. The Introduction contains the first appearance of the syllogistic mnemonic verse ‘Barbara, Celarent…’, which Augustus de Morgan described as “magic words … more full of meaning than any that ever were made”, and Sherwood may even have been the inventor of the verse, though references to individual names appear earlier (Kretzmann 1966, pp. 66–67).
Sherwood’s treatise on syncategorematic terms has long been held to be if not the earliest such treatise, then the earliest still accessible (Boehner 1952, p. 7). The text was first edited by O’Donnell (1941), and this edition along with the Paris MS was the basis of Kretzmann’s 1968 translation into English. O’Donnell’s edition has since been superseded by the critical edition of Kann and Kirchhoff (2012), which also includes a translation into German. Kirchhoff (2008) is an extensive discussion and commentary on the Syncategormeta.
Three other logical treatises follow the Introductiones and the Syncategoremata in the Paris manuscript, which have as a result been tentatively attributed to Sherwood. The first is a treatise on insolubles, ff. 46–54, edited by Roure (1970), and the second a treatise on obligationes found in Paris, Bibl. Nat. 16617. This text was edited by Green (1963), who tentatively attributed it to Sherwood. The third is the text Petitiones Contrariorum, edited by de Rijk (1976), covering puzzles arising from hidden contradictions in sets of premises. Sherwood may also be the author of the Fallaciae magistri Willelmi “Fallacies, of Master William” preserved in British Museum, King’s Library MS 9 E XII, as well as the treatise ascribed to Richard of Sherwood noted above.
Three further treatises have previously also been attributed to Sherwood, but the evidence for their attribution is less clear: the commentary on the Sentences of Peter Lombard noted above, a Distictiones theologicae, and a Concionces, or collection of sermons (Kretzmann 1968, p. 4).
2. Important doctrines
Along with Peter of Spain, Lambert of Auxerre, and Roger Bacon, William of Sherwood was one of the first terminist logicians, working in a context where the newly discovered and translated Aristotelian material of the 12th century had become fully integrated into the logical and philosophical curricula through the works of people such as John le Page (Uckelman & Lagerlund, 2016). The terminist period of logic was marked by the development of logical genres and techniques that go beyond Aristotle and mere commentaries on his works. The two primary branches of terminist logic are the study of the properties of terms and the study of the meaning and function of syncategorematic words. Sherwood’s Introduction picks up the first of these two branches in its fifth chapter, and his Syncategoremata deals with the second. The remainder of the Introductiones is devoted to the standard Aristotelian material: Chapter One on statements corresponds to On Interpretation; Chapter Two on predicables to the Categories; Chapter Three on syllogisms to the Prior Analytics; Chapter Four on dialectical reasoning to the Topics; and Chapter Six on sophistical reasoning to the Sophistical Refutations. We will focus our attention in this article on the unusual or distinctive aspects of his logical and semantic theory, as found in Chapter Five of the Introduction and in the Syncategoremata.
2.1. Modality
In his Introduction, Sherwood gives two definitions for ‘mode’, depending on whether the term is being used broadly or strictly: “Broadly speaking, a mode is the determination of an act, and in this respect it goes together with every adverb”, while strictly speaking we count not all adverbs as modes but only those which determine the inherence of the predicate in the subject (Kretzmann 1966, p. 40). Thus, on the broad conception of ‘mode’, both “Socrates is necessarily running” and “Socrates is swiftly running” count as modal statements, but on the narrow conception, only the former does. The six modes are ‘true’, ‘false’, ‘possible’, ‘contingent’, ‘impossible’, and ‘necessary’, though “the first two do not distinguish a modal proposition from an assertoric statement” (Kretzmann 1966, pp. 40–41). The other four modes give rise to properly modal propositions, and in statements expressing these propositions, the associated modal adverbs are ‘possibly’, ‘contingently’, ‘impossibly’, and ‘necessarily’. Each of these modal adverbs is a syncategorematic term; and in the Syncategoremata, Sherwood devotes an entire chapter to necessario (‘necessarily’) and contingenter (‘contingently’).
Here it must be noted that Sherwood’s views of modality differ significantly from modern views. Modern modal logic interprets modes in a nominal way, e.g., ‘necessary:’, ‘impossible:’, etc. But Sherwood is reluctant to admit a statement such as “That Socrates is running is necessary” as genuinely modal (Kretzmann 1966, p. 43), instead viewing this as an assertoric categorical statement predicating ‘necessary’ of “that Socrates is running”. Similarly, “Socrates is running necessarily” does not count as a modal statement, because here ‘necessarily’ modifies ‘running’, not “the inherence of the predicate in the subject”. The only genuinely modal construction is that exhibited by “Socrates is necessarily running” (Kretzmann 1966, p. 42). The importance of the adverbial construction, where the modal adverb modifies the inherence of the predicate with the subject, is emphasized in the discussions of modal adverbs in Syncategoremata, which include not only the chapter mentioned above but also analyses of how modal adverbs interact with other syncategorematic terms such as “only”, “unless”, and “if” (Uckelman 2020, §5).
Since Aristotle it was standard practice to note that ‘possible’ can be used in two ways. In the first ‘possible’ is compatible with ‘necessary’, but in the second, that which is necessary is not (merely) possible. This second way is usually called ‘contingent’. Sherwood mentions this distinction, but goes on to say that he will be using it in a broader sense, in which possibility is compatible with necessity (Kretzmann 1966, p. 41). However, he makes a further distinction, which he does maintain, between the two ways that ‘impossible’ and ‘necessary’ can be used. These different ways are expressed in temporal notions:
[impossible] is used in one way of whatever cannot be true now or in the future or in the past; and this is ‘impossible per se’ … It is used in the other way of whatever cannot be true now or in the future although it could have been true in the past … and this is ‘impossible per accidens’. Similarly, in case something cannot be false now or in the future or in the past it is said to be ‘necessary per se’ … But it is ‘necessary per accidens’ in case something cannot be false now or in the future although it could have been [false] in the past (Kretzmann 1966, p. 41).
Sherwood says that the reason it is important to separate modal propositions from assertoric ones is that
[s]ince our treatment is oriented toward syllogism, we have to consider them under those differences that make a difference in syllogism. These are such differences as … modal, assertoric; and others of that sort. For one syllogism differs from another as a result of those differences (Kretzmann 1966, p. 39).
Despite this, there is “no treatment of modal syllogisms in any of the works that have been ascribed to Sherwood” (Kretzmann 1966, p. 39, fn. 58). For more on Sherwood’s account of modality, see (Uckelman 2008).
2.2. Properties of terms
The theory of the “properties of terms” forms the basis of medieval semantic theory and provides an account of how terms function within the broader context of sentences, as well as how these different functions can account for the different rules governing inference. Sherwood identifies the four main properties of terms as (1) signification; (2) supposition; (3) copulation; and (4) appellation (Kretzmann 1966, p. 105). In this classification he differs from other accounts which mention (1) signification; (2) supposition and copulation; (3) ampliation and restriction; (4) appellation; and (5) relation.
Sherwood defines ‘signification’ as “a presentation of the form of something to the understanding”, a definition harking back to 12th-century semantic theory (Kretzmann 1966, p. 105, fn. 2). Supposition and copulation are symmetrically related to each other; ‘supposition’ is “an ordering of the understanding of something under something else” while ‘copulation’ is “an ordering of the understanding of something over something else” (Kretzmann 1966, p. 105). Only substantive nouns, pronouns, and definite descriptions can have supposition, while only adjectives, participles, and verbs can have copulation (Kretzmann 1966, p. 106).
Finally, ‘appellation’ is “the present correct application of a term — i.e., the property with respect to which what the term signifies can be said of something through the use of the verb ‘is’” (Kretzmann 1966, p. 106). That is, the appellata of a term are the presently existing things of which the term can currently be truly predicated. Appellation is between supposition and copulation: Substantive nouns, adjectives, and participles can have appellation, but pronouns and verbs cannot (Kretzmann 1966, p. 106).
The central notion of these three is supposition, and the majority of the chapter is devoted to the division of supposition into its various kinds:
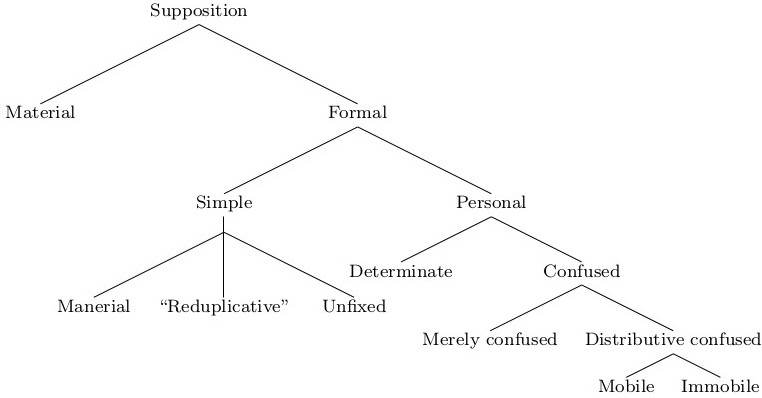
For a discussion of most of the notions in this division as well as a comparison of Sherwood’s views to those of his 13th-century contemporaries and his 14th-century posterity, see the article Medieval Theories: Properties of Terms. We briefly comment on ‘manerial’ supposition, a type which does not appear outside of Sherwood. Some have considered manerialis an error for materialis, and considered Sherwood to have been talking here about material supposition (Grabmann 1937). However, the manuscript shows n rather than t, and the type of supposition is not the same as the material supposition, which is distinguished from formal supposition, but is itself a type of formal supposition. Sherwood says that manerial supposition is a type of simple supposition in which “a word can be posited for its significatum without any connection with things”, and he gives as an example “Man is a species”. The explanation is that this is manerial supposition because ‘man’ “supposits for the specific character in itself” (Kretzmann 1966, p. 111). The notion of maneries meaning ‘character, way, mode, manner’ can be found in 12th-century discussions of universals; for example, John of Salisbury notes that Joscelin, Bishop of Soissons, says that sometimes the words genus and species “are to be understood as things of a universal kind” and sometimes he “interprets them as modes (maneries) of things” (Hall, Book II, ch. 17, p. 84). John says he does not know where Joscelin got such a distinction, but it occurs in Abelard and in the 12th-century Fallacie Parvipontane (Hall, Book II, ch. 17, p. 84, fnn. a, b; de Rijk 1962, pp. 139, 562).
2.3. Semantics of universal affirmatives
Statements are composed of two types of parts: principal and secondary. The principal parts of a statement are the nouns and verbs, that is, the subjects and predicates whose properties are the focus of the first branch of terminist logic. The secondary parts are those that remain: “the adjectival name, the adverb, and conjunctions and prepositions, for they are not necessary for the statement’s being” (Kretzmann 1968, p. 13). These are words which do not have signification in themselves, but only in conjunction with other significative words, namely the subject and predicate (Kretzmann 1966, p. 24). Because these words do not have signification in themselves, they do not have any of the usual properties of terms — supposition, copulation, and ampliation. Nevertheless, they still have a significative function. Explaining this function is the focus of Sherwood’s treatise on syncategorematic terms.
It is in this treatise that we can see evidence for what some have said is a distinctively English approach to syncategorematic terms (Uckelman & Lagerlund 2016). Sherwood and his English contemporary Bacon both consider distributive terms such as ‘every’ to be syncategorematic, while in continental works such as those by John le Page, Peter of Spain, and Nicholas of Paris, distributive terms are usually considered in summary treatises in the chapter on distribution (a chapter found in no English summary) (Braakhuis 1981, pp. 138–139). In his consideration of ‘every’, Sherwood argues that propositions involving ‘all’ require that there be at least three things for which the predicate term truly stands:
Rule [II] The sign ‘every’ or ‘all’ requires that there be at least three appellata (Kretzman 1968, p. 23).
(Remember that an appellatum is something which both exists and which the subject stands for or refers to.) The justification for this is taken from Aristotle, who Sherwood quotes as saying “Of two men we say that they are two, or both, and not that they are all” (Kretzmann 1968, p. 23). That is, if there were fewer than three, it would be more appropriate to say ‘Both’ or ‘One’ rather than ‘All’.
Sherwood is also noteworthy for being the first logician we know of to treat ‘is’ as a syncategorematic term (Kretzmann 1968, p. 90). He argues that ‘is’ is equivocal, in that it can indicate either (1) actual being (esse actuale) or (2) habitual being (esse habituale) (Kretzmann 1968, p. 92, Kretzmann 1966, p. 125; Kretzmann translates habituale as ‘relational’ in Kretzmann 1966 and as ‘conditional’ in Kretzmann 1968). As a result, the sentence “Every man is an animal” is ambiguous. When ‘is’ is taken to indicate actual being, “Every man is an animal” “is false when no man exists” (Kretzmann 1968, p. 93). When ‘is’ is taken to indicate habitual being, then “insofar as [”Every man is an animal“] is necessary it has the force of this conditional: ‘if it is man it is an animal’” (Kretzmann 1966, p. 125). In analyzing universal affirmative categorical sentences in this way, Sherwood can be seen as an ‘early adopter’ of our modern truth conditions for these sentences. A consequence of this view is a commitment to the existence of possibilia, things that could exist but which do not; such possibilia have a diminished sort of being (esse diminutum) (Kretzmann 1968, p. 93). This was an unusual position in the thirteenth century (Knuuttila 1993), and it was later denounced by William of Ockham (Freddoso & Schuurman 1980, p. 99).
3. Influence
Bacon’s approbation of Sherwood is not the only explicit reference we have to him by his contemporaries. The copy of Chapter Five of the Introduction found in MS Worcester Cath. Q. 13 mentioned earlier is followed by a collection of anonymous notes (also edited in Pinborg & Ebbesen 1984 and there called the Dubitationes). Pinborg and Ebbesen argue that these lecture notes, composed either for a teacher’s or a student’s use, are unlikely to have been written in response to lectures given in the 1290s, i.e., when the manuscript was copied, but rather date from the 1260s or the 1270s, favoring a date around 1270 (Pinborg and Ebbesen 1984, p. 104). This text thus provides evidence that Sherwood’s works continued to be taught and circulated.
Beyond these explicit mentions, it is clear that Sherwood’s works were widely influential among logicians at the University of Paris in the second half of the 13th century. The most direct line of influence runs from William of Sherwood to his much better-known colleague Peter of Spain. It was for many years believed that Peter was the first person to translate Psellus’s text (Mullinger 1873, p. 176), prior to the rediscovery of Sherwood’s Introduction, which pre-dates Peter by two decades and which is closer to Psellus’s work. Peter’s Summary of Logic is clearly indebted to Sherwood. Kretzmann notes that “many of the features of the Summulae that made it far and away the most popular logic textbook in the Middle Ages seem quite plainly to have developed as modifications of more difficult discussions and less felicitous mnemonic devices in the Introductiones” (Kretzmann 1968, p. 6). On the other hand, Sherwood appears to have been influenced by Peter’s treatise on syncategorematic terms in writing his own; Kretzmann provides a summary of passages in Sherwood’s treatise which “can be read as allusions to positions taken by Peter” (1968, p. 7). Other influences can be found in Albert the Great, who used Sherwood’s notion of appellation rather than Peter of Spain’s (Kretzmann 1966, p. 5), and Thomas Aquinas, whose analysis of modal propositions follows Sherwood (Kretzmann 1966, p. 5; Uckelman 2008).
Though Sherwood’s indirect influence on the development of logic and semantics, via his influence on Peter of Spain, should not be underestimated, his direct influence beyond the 13th century was more minimal, in part because the influence of Peter of Spain was so great. In the 14th century, any influence Sherwood’s approach to the properties of terms might have still had was almost entirely eclipsed by figures such as William of Ockham, John Buridan, and Albert of Saxony (Bos 2011, p. 773).
Bibliography
- Boehner, Philotheus, 1952, Medieval Logic: An Outline of Its Development from 1250 to c. 1400, Manchester: Manchester University Press.
- Bos, E. P., 2011, “Kirchhoff, Raina, Die “Syncategoremata” des Wilhelm von Sherwood: Kommentierung und historische Einordnung,” Speculum 86, no. 3: 773–775.
- Braakhuis, H. A. G., 1981, “English Tracts on Syncategorematic Terms from Robert Bacon to Walter Burley”, in H. A. G. Braakhuis, C. H. Kneepkens, and L. M. de Rijk, eds. English Logic and Semantics: From the End of the Twelfth Century to the Time of Ockham and Burleigh, Nijmegen: Ingenium Publishers.
- Brands, Hartmut and Christoph Kann (eds. and trans.), 1995, William of Sherwood. Introductiones in Logicam / Einführung in die Logik, Hamburg: Felix Meiner Verlag.
- Freddoso, Alfred J. and Henry Schuurman (trans.), 1980, William of Ockham. Ockham’s Theory of Propositions: Part II of the Summa Logicae, Notre Dame: University of Notre Dame Press; reprinted St. Augustine’s Press, 1998.
- Grabmann, Martin (ed.), 1937, William of Sherwood, Introductiones in Logicam (Introduction to Logic), München: Verlag der Bayerischen Akademie der Wissenschaften.
- Green, Romuald, 1963, An Introduction to the Logical Treatise De Obligationibus, With Critical Texts of William of Sherwood [?] and Walter Burley, Ph.D. Dissertation, Katholieke Universiteit Leuven. (A revised version of this essential but unpublished dissertation has widely circulated in manuscript form under the title The Logical Treatise ‘De obligationibus’: An Introduction with Critical Texts of William of Sherwood and Walter Burley.)
- Hall, J. B. (trans.), 2013, John of Salisbury. Metalogicon, Turnhout: Brepols.
- Kann, Christoph and Raina Kirchhoff (eds.), 2012, William of Sherwood. Syncategoremata, Hamburg: Felix Meiner Verlag.
- Kirchhoff, Raina, 2008, Die “Syncategoremata” des Wilhelm von Sherwood: Kommentierung und historische Einordnung, Studien und Texte zur Geistesgeschichte des Mittelalters, 98, Leiden and Boston: Brill.
- Knuuttila, Simo, 1993, Modalities in Medieval Philosophy, London: Routledge.
- Kretzmann, Norman (ed.), 1966, William of Sherwood. William of Sherwood’s Introduction to Logic, Minneapolis: University of Minnesota Press.
- Kretzmann, Norman (ed.), 1968, William of Sherwood. Treatise on Syncategorematic Words, Minneapolis: University of Minnesota Press.
- Mullinger, James Bass, 1873, The University of Cambridge: From the Earliest Times to the Royal Injunctions of 1535, Cambridge: Cambridge University Press.
- O’Donnell, J. Reginald, 1941, “The Syncategoremata of William of Sherwood”, Medieval Studies, 3: 46–93.
- Pinborg, Jan and Sten Ebbesen, 1984, “Thirteenth Century Notes on William of Sherwood’s Treatise on Properties of Terms, an Edition of Anonymi Dubitationes et Notabilia circa Guilelmi de Shyreswode Introductionem Logicalium Tractactum V from MS Worcester Cath. Q. 13”, Cahiers de l’Institut du Moyen Âge Grec et Latin, 47: 104–141.
- de Rijk, L. M., 1962, Logica Modernorum (Volume 1): On the Twelfth Century theories of Fallacy, Assen: Van Gorcum.
- de Rijk, L. M., 1976, “Some Thirteenth Century Tracts on the Game of Obligation III”, Vivarium, 14: 26–49.
- Roure, Marie Louise, 1970, “La problématique des propositions insolubles du XIIIe siècle et du début du XIVe, suivie de l’édition des traités de William Shyreswood, Walter Burleigh et Thomas Bradwardine”, Archives d’Histoire Doctrinale et Littéraire du Moyen Age, 37: 205–326.
- Uckelman, Sara L., 2008, “Three 13th-Century Views of Quantified Modal Logic”, in Carlos Areces and Rob Goldblatt, Advances in Modal Logic (Volume 7), London: College Publications, 389–406.
- Uckelman, Sara L., 2020, “William of Sherwood on Necessity and Contingency”, in Nicola Olivetti, Rineke Verbrugge, Sara Negri, and Gabriel Sandu (eds.), Advances in Modal Logic (Volume 13), London: College Publications, pp. 597–612.
- Uckelman, Sara L. and Henrik Lagerlund, 2016, “Logic in the Thirteenth Century”, in Stephen Read and Catarina Dutilh Novaes (eds.), Cambridge Companion to Medieval Logic, Cambridge: Cambridge University Press.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.


