
Photo from the Hans Reichenbach Collection, reproduced by permission of the University of Pittsburgh. All rights reserved.
Hans Reichenbach
Described as perhaps “the greatest empiricist of the 20th century” (Salmon, 1977a), the work of Hans Reichenbach (1891–1953) provides one of the main statements of empiricist philosophy in the 20th century. Provoked by the conflict between (neo-) Kantian a priorism and Einstein’s relativity of space and time, Reichenbach developed a scientifically inspired philosophy and an uncompromisingly empiricist epistemology. He was literate in the physical science of his time, and acquainted with many of its most eminent practitioners. Criticism and justification of scientific methodology formed the core of almost all his philosophical efforts, which he promoted in a crescendo of books, in the journal Erkenntnis, which he founded and edited with Rudolf Carnap, and within a group of philosophers, mathematicians and scientists he led in Berlin. His commitment to objectivity and realism in science together with his probabilistic justification of belief in scientific results carried philosophical and technical difficulties that shaped much of the subsequent debate in philosophy of science. Reichenbach’s contributions cover large swathes of formal philosophy, especially in philosophy of physics, logic, induction and the foundations of probability, and his later work encompassed linguistics, philosophical logic, and ethics. The fruits of some of his insights are only belatedly having their full impact. For example, several of the recent accounts of causality employ ideas that can be traced to Reichenbach’s The Direction of Time.
Partitioning the work of a philosopher with views about almost everything is indispensable in a retrospective, but in Reichenbach’s case separation is especially artificial. From 1915 until 1953, most of his philosophical essays entangle issues and doctrines about probability, causality, physics, epistemology and metaphysics. Reichenbach’s ideas about causality and probability are so intertwined that it makes little sense to discuss them separately. Unavoidably, therefore, different aspects of the same works are discussed in several sections of the following essay. Reichenbach’s views on all of these topics changed so radically over time that there is no one “Reichenbach system,” and we therefore offer a synoptic history of his views within each topic. All of our citations are from the English editions of his publications, where available.
- 1. Life
- 2. Causality and Probability
- 3. Epistemology and Metaphysics
- 4. Philosophy of Physics
- 5. Logic and Modality
- 6. Ethics and Free Will
- 7. Reichenbach’s Influence
- 8. Retrospective
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Life
Born in Hamburg, Germany, in 1891, Hans Reichenbach was the second of four children of a half-Jewish but baptized father and a non-Jewish mother. In secondary school and at university he was active in the socialist student movement. From 1910 to 1911 he studied civil engineering at the Technische Hochschule in Stuttgart, and then moved among Berlin, Munich and Göttingen, studying physics, philosophy and mathematics with some of the eminences of the time, including Ernst Cassirer, Max Planck, Arnold Sommerfeld and David Hilbert.[1] He wrote his doctoral dissertation largely on his own after the neo-Kantian Paul Natorp would not accept him as his student. After searching for alternative advisors, his dissertation was finally accepted by Paul Hensel, a philosopher, and Max Noether, a mathematician, in 1915 in Erlangen. Reichenbach was conscripted into the army while completing his thesis. He served in the German army signal corps on the Russian front until a serious illness sent him back to Berlin in 1916. He was relieved from active military duty in 1917 to work as an engineer for a firm specializing in radio technology. In Berlin, Reichenbach attended Albert Einstein’s lectures on relativity and statistical mechanics, which influenced him profoundly, and inaugurated a life-long friendship between the two men. He wrote several popular articles defending Einstein, especially in the context of the observations of the solar eclipse of 1919 confirming the predictions of the general theory of relativity.
In 1920 Reichenbach became an instructor in physics, and eventually associate professor, at the Technische Hochschule in Stuttgart. The Theory of Relativity and A Priori Knowledge (1920f) was accepted as his habilitation in physics. In this period Reichenbach married Elizabeth Lingener and they had two children, Hans Galama in 1922 and Jutta in 1924. While in Stuttgart he developed contacts with Moritz Schlick, Rudolf Carnap and Erwin Schroedinger. In 1926, after much back and forth, he assumed a teaching position in “natural philosophy” at the University of Berlin, where he remained until Hitler came to power in 1933. During this time Reichenbach organized discussion groups on scientific philosophy, similar to those of the Vienna Circle (see entry on Vienna Circle). The group around Reichenbach that developed out of the Society for Empirical Philosophy and became known as the Berlin Group included Kurt Grelling, Kurt Lewin, Richard von Mises and later Carl Hempel, Reichenbach’s student. Together with members of the Vienna Circle, Reichenbach initiated the publication of the journal Erkenntnis in 1930 as a forum for scientific philosophy. Reichenbach and Carnap were the only editors after Schlick resigned in reaction to Reichenbach’s opening article (see Section 4.4 below). In addition (and also for financial reasons), Reichenbach was a frequent contributor of popular essays and a regular radio lecturer on scientific topics.
With Hitler’s elevation, the views and methods of the Berlin Group and Vienna Circle were branded Jewish philosophy, and Reichenbach—who counted as Jewish to the National Socialists and was in any case considered undesirable given his socialist writings as a student—was dismissed from his university position and from radio work. He moved to Istanbul in 1933, where, as part of his efforts to westernize Turkey, Mustafa Kemal (Atatürk) had established a new university to attract intellectuals fleeing Europe. Reichenbach was joined there by 32 other German professors, notably Richard von Mises, the mathematician whose views on probability must have influenced Reichenbach, and Erwin Freundlich. Freundlich had been Einstein’s assistant in Berlin on matters astronomical, led an unsuccessful German expedition to Russia to measure the gravitational deflection of starlight at the 1914 solar eclipse (the members of the expedition became prisoners of war!), and later joined the “Einstein Observatory” in Potsdam.
Under a five-year contract which prevented him from accepting a position at New York University arranged by Einstein and Sidney Hook, Reichenbach remained in Turkey until 1938, when, through the efforts of many people, most notably Charles Morris, Reichenbach moved to the University of California, Los Angeles (UCLA) with his family. Hiking in the Swiss Alps shortly before his move to Los Angeles, Reichenbach suffered a heart attack, which prevented him from teaching during the first months of his American appointment. (Reichenbach was an avid hiker and skier, but not physically impressive. His student, Cynthia Schuster, describes his appearance around 1950 this way: “short, almost rotund, stubby hands and feet, round face, snub nose, thick glasses, false teeth, a hearing aid, and a thin high-pitched speaking voice.” (Reichenbach 1978, vol. I) His influence on students, she says, was a case of mind over matter.) With the US entry into World War II in 1941, Reichenbach—as a resident German alien—was kept under effective house arrest, allowed to leave only to work and for medical purposes until he obtained American citizenship in 1943. During the war, Reichenbach was engaged in helping to move members of his family out of Germany and to secure positions for colleagues at UCLA, in particular members of the Frankfurt School (Theodor Adorno, Max Horkheimer), who with Berthold Brecht and Thomas Mann became part of Reichenbach’s German intellectual circle in Los Angeles. In 1939 he was reunited with Maria Moll, who had been his colleague in Istanbul. They married in 1946, the day after her divorce. Despite bitter discussions at UCLA about the McCarthy era California Loyalty Oath, in which each faculty member had to attest that they were not members of the Communist party, we are not aware of any written objections from Reichenbach. He signed the oath in 1949/50, apparently unwillingly, as an understanding letter from Rudolf Carnap suggests (McCumber 2016, p.52). Reichenbach’s untimely death from another heart attack on April 9, 1953, prevented him from presenting the William James Lectures at Harvard in the fall of the same year, and also prevented his inclusion in a planned volume of Living Philosophers in the series edited by Arthur Schilpp.
Further Reading. Much more detail about Reichenbach’s life can be found in the excellent biography by Gerner (1997). Volume I of Reichenbach (1978) contains memories and comments from many of Reichenbach’s friends, colleagues, students and relatives. Further biographical detail can be found in Salmon’s introduction (translated to German by Maria Reichenbach) to volume 1 of Reichenbach (1977), in Salmon (1979), in Maria Reichenbach (1994), in Padovani (2008) and Kamlah (2013), while The Hans Reichenbach Collection (linked into the Other Internet Resources section below) at the University of Pittsburgh contains a wealth of autobiographical notes, in particular references HR 014-33-08 and HR 044-06-21 to HR 044-06-26. Hoffman (2007) and Milkov (2013) describe the historical developments of the Berlin Group and Irzik (2011) provides the same for Reichenbach’s move to Istanbul. Verhaegh (2020) traces in detail Reichenbach’s move to Istanbul and the decisions and hurdles that eventually took him to the U.S.
2. Causality and Probability
2.1 Doctoral Thesis
Reichenbach’s doctoral thesis, The Concept of Probability in the Mathematical Representation of Reality (1915b), contains many of the themes that concerned him throughout his life, and anticipated in some detail 21st century philosophical discussions of probability relations between microscopic and macroscopic systems. Indeed, the development of his ideas about causality and probability from 1915 until the end of his life can be seen as a series of reexaminations and reformulations of issues the thesis implicitly posed and the solutions it explicitly offered.
The thesis develops an account of probability appropriate for scientific inference. It presents an argument to supplement what Reichenbach understands to be Kant’s transcendental principle of causality with a transcendental principle of probability. In Reichenbach’s reading of Kant, the “principle of causality” asserts that every event is preceded by a cause that determines it according to some universal law (see the discussion of Kant’s principle in Section 2 of the entry on Kant and Hume on Causality). The principle is “transcendental” because it cannot be empirically established, but is instead a precondition for the very possibility of empirical knowledge. Reichenbach’s claim is that there is a principle of probability that has an equal status: it cannot be empirically established, but it is a precondition of empirical knowledge. It states that events are governed by a probability distribution.
Reichenbach considers, and rejects, the subjective interpretation of probability advocated by the then prominent philosopher and psychologist Carl Stumpf (1892a, b), and, less emphatically, the attempt at an objective interpretation advocated by Johannes von Kries (1886), a physiologist who had studied with Hermann von Helmholtz. According to Reichenbach, von Kries’s account of probability needs to be freed from the principle of insufficient reason—that mutually exclusive events of which we have no knowledge that would determine differential probability are equally probable. As a subjective principle, Reichenbach claimed, it had no place in science. Reichenbach insists on an “objective” interpretation of probability—in the Kantian sense as about the world of experience—for which probability statements are synthetic, but not verifiable, claims about the empirical world. His task, as he sees it, is to demonstrate that probabilistic statements are supported by a claim—the “existence of a probability function”—which is a transcendental principle that is necessary, and in combination with causal principles sufficient, for empirical knowledge.
Reichenbach’s technical argument is an adaptation of Henri Poincaré’s results on probability functions and what have since come to be called “strike ratios” (Poincaré, 1912, pp. 148–150). By considering events collected in a histogram, in which alternate equally narrow columns are black and white, Reichenbach argues that as the number of (independent) events increases (and the width of the columns decreases) the ratio of black to white events within any interval of the abscissa will approximate 1. Reichenbach’s general idea is that if a variable X is divided into two or more classes of very small intervals of equal width (in X units) juxtaposed in a definite order and proportion, then there will be a probability for the occurrence of a value of X within any particular class that is invariant over all Riemann integrable probability distributions for X. (The Riemann integral of a function describing a curve is defined as the limit of the sum of rectangles touching the curve as their width approaches 0.)
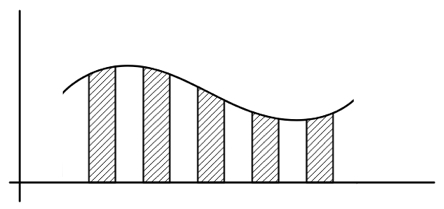
Reichenbach extends the analysis to error probabilities for physical measurements. He then argues that since all physical measurements are subject to error, knowledge of natural laws is possible only if errors occur subject to a probability distribution, a proposition that is synthetic but cannot be established empirically. Empirical knowledge thus requires both an a priori principle of causality for individual events and an a priori principle of probability to ensure that individual events can be aggregated into general laws. No explicit interpretation of probability is forwarded, although Reichenbach implies that probability claims are about frequencies of causally independent events—a notion for which probability theorists would later substitute the idea of independent, identically distributed events (see the entry on probabilistic causation)— in observed and unobserved collections of cases.
Further Reading. The thesis with an introduction to the arguments can be found in Reichenbach (2008). Re-statements and slight variations of the arguments in the thesis can also be found in Reichenbach (1920c), Reichenbach (1920e) and to a lesser extent in Reichenbach (1930g) and chapter 9 of Reichenbach (1949f). A synopsis is also given in Padovani (2011), while Eberhardt (2011) provides a critical assessment of the thesis.
2.2 Views Prior to The Theory of Probability
Reichenbach’s allegiance to Kantian formulations waxed and waned and transformed over time, but while the terminology changed, Reichenbach long retained the essential claim of his doctoral thesis that the establishment of any empirical law requires a superempirical presupposition about probability. In 1920, the argument and conclusions of the thesis were repeated with little qualification or variation in two essays, “The Physical Presuppositions of the Calculus of Probability”, and “A Philosophical Critique of the Probability Calculus”. Again in “Causality and Probability”, in 1930, Reichenbach reprises the claims of his doctoral thesis, but substitutes the “principle of induction”—that observed frequencies will continue to hold in new cases—for the “principle of probability.” The principle of induction is not given an explicitly a priori basis, the possibility of which Reichenbach had come to doubt when studying with Einstein (see Reichenbach, 1920f). Instead, it is justified by an uneasy mixture of loose convergence arguments (foreshadowing the straight rule, see below) and psychological habit. Without attribution, he dismisses a “conventionalist” account of the principle of induction, expressed in nearly Kantian terms, as “the principle of induction is not a statement about the physical world, but merely constitutes an ordering principle of science.” He argues that such an account does not “justify” scientific preferences for simpler hypotheses (1930g, see Reichenbach 1978, vol. II, p. 340–341). Arbitrary convention could choose any scientific hypothesis that captures the phenomena, but a descriptively accurate account of theory selection in science must explain why simpler theories should be preferred. The justification of the preference for simpler hypotheses remains unexplained in “Causality and Probability”, and Reichenbach’s own conclusion seems to be essentially the Kantian principle he rejects, supplemented with an attempt to prove that the principle of induction is unchallengeable because, in his view, probability claims are generalizations over as yet unobserved cases and therefore presuppose the principle of induction:
We found that a probability statement is meaningful only if the principle of induction holds; therefore the statement that the probability laws do not hold is itself meaningless unless the principle of induction holds. To say that probability laws do not hold is equivalent to predicting that the observed relative frequency of sequences of events will not be preserved in the future, that the regularity implied by the principle of induction does not hold—and this statement has empirical meaning only if it can be decided inductively, i.e., if the principle of induction holds. The statement that probability laws do not hold is self-contradictory and makes no sense. (1978, vol. II, p. 343)
In a further break with the Kantian tradition, the role of causation as conceptually primitive is reconsidered. It is difficult to pinpoint Reichenbach’s position between 1915 and 1935 since his writings mix epistemic and metaphysical issues. In his thesis (1915b) and in “Stetige Wahrscheinlichkeitsfolgen” (1929L) Reichenbach is committed to individual deterministic causal events. In “The Causal Structure of the World” (1925d) probability is regarded as the more fundamental concept. In later years Reichenbach often cited this paper as an anticipation of the indeterminism of quantum theory, because his account allows the possibility that finer and finer measures will not converge to deterministic laws (see Gerner, 1997, p. 153). In “Causality and Probability” (1930g) causality explicitly refers to regularities in populations rather than to particular events, a view whose source Reichenbach attributes to Ludwig Boltzmann’s development of the theory of gases. The separation of causality and probability, and the recasting of causality as a higher level concept, required that Reichenbach find a new foundation for probability. Presumably due to the influence of his colleague Richard von Mises, Reichenbach moved towards a view of probability as a property of sequences.
Reichenbach’s 1925 essay “The Causal Structure of the World” (1925d) is also an early attempt to account for the direction of time in terms of causal and probabilistic asymmetries. Reichenbach there introduces the notion of a “probability implication” with 10 axiom schemes on propositional variables involving both material implication and a new 2-place probability implication connective. The axioms are evidently meant to supplement those of propositional logic. No rules of inference are specified, but substitution and modus ponens are used. The axioms do not guarantee that a probability implication, a ⊇ b[2], is the conditional probability of b given a, or even that the consequents of a collection of probability implications with a as antecedent satisfy the axioms of finite probability. Interpretation is difficult, since Reichenbach both asserts that the probability of the consequent in a probability implication can be between 0 and 1 inclusive (1925d, 1978, vol. II, p. 89), but then disallows a probability implication because the consequent has probability 0 (p. 92). Reichenbach’s thought seems to be that a ⊇ b asserts that in circumstance a, b has a well defined probability, that is, a specifies something like what Ian Hacking (1965) later called a “chance setup,” or as Reichenbach might have put it, implies the existence of a probability function for {b, ~b}. Reichenbach uses the operation very much in that way in his 1925 discussion of the direction of time, which he thinks can be founded on cases in which a ⊇ b is true but b ⊇ a is false. Even under this reading some of his axiom schemes have false instances, e.g., (a ⊇ b) ⊃ (a.c ⊇ b), where the dot is ordinary conjunction. (The claim that b has a probability distribution in context a does not necessarily imply that b has a probability distribution in context a conjoined with context c, since c might make a distribution impossible.) Revised, probability implication later became a foundational notion of Reichenbach’s theory of probability and the central concept of his approach to inductive logic.
Further Reading. For Reichenbach’s views on causality see also the discussion of “The Direction of Time” below and the separate entry on Reichenbach’s Common Cause Principle.
2.3 The Theory of Probability (1935, 1949)
Reichenbach continued to revise and elaborate his ideas about probability in a series of papers in the early 1930s[3] until, in 1935, his The Theory of Probability provided a fuller statement of his developed view. Surprisingly, Reichenbach does not acknowledge help from Richard von Mises, his colleague in Berlin and Istanbul in the period and the mathematician whose views on the foundations of probability were closest to his own and are often discussed in the book. He does attribute part of the mathematical work in the book to Valentine Bargmann, who after finishing his doctorate in physics in Berlin fled to Switzerland in 1933 and later became an assistant to von Neumann and to Einstein at the Institute for Advanced Study, from where in the 1940s he also assisted Reichenbach’s work on quantum theory.
It is fair to say that The Theory of Probability was not well received, drawing intense criticism from Karl Popper (1934), who had read Reichenbach’s papers presenting a frequentist interpretation of probability, C.I. Lewis (1952), Bertrand Russell (1948), and Ernest Nagel (1936, 1938). Kolmogorov’s measure theoretic axioms for probability, which appeared in 1933, soon overshadowed Reichenbach’s formulation of the theory of probability.
The Theory of Probability uses class terms—A, B, C—and individual variables—x, y, z—as well as real variables—p, q, u, r, w. Distinct individual variables are (unnecessarily) sometimes and sometimes not associated with distinct class names, but Reichenbach’s formulae without iterated probability conditionals can be read as universally quantified with a single individual variable. The earlier 10 axiom schemes for probability implication (1925d) are replaced by 4 axiom schemes expressed in Reichenbach’s abbreviated form as (1949f, p. 53–65):
- Univocality: (p ≠ q) ⊃ [(A ⊇p B) . (A ⊇q B) ≡ (~A)]
- Normalization:
- (A ⊃ B) ⊃ ∃p[(A ⊇p B) . (p = 1)]
- ~~A . (A ⊇p B) ⊃ (p ≥ 0)
- Addition: [(A ⊇p B) . (A ⊇q C) . (A.B ⊃ ~C)] ⊃ ∃r[(A ⊇r (B ∨ C)) . (r = p+q)]
- Multiplication: [(A ⊇p B) . (A.B ⊇u C)] ⊃ ∃w[(A ⊇w B.C) . (w = p∗u)]
Reichenbach’s intent with formula I is to say that where it exists, the probability has a unique value. Axiom II is meant to ensure that the probabilities conditional on a nonempty set have values between 0 and 1 inclusive. Axiom III is Reichenbach’s version of the requirement that the probability of the union of mutually exclusive events is the sum of their probabilities. Axiom IV is essentially the chain rule of probability: P(CB | A) = P(C | BA) P(B | A). Axiom I is implicit in the Kolmogorov axioms (see Section 1 (“Kolmogorov’s Probability Calculus”) in the entry on interpretations of probability) since probability is taken to be a real valued function. Axiom II corresponds to Kolmogorov’s first and second axioms, that probability values are bounded between 0 and 1 inclusive. Axiom III amounts to finite additivity because Reichenbach’s logic does not have infinite disjunctions: it is a finite restriction of Kolmogorov’s third axiom, which postulates additivity of probabilities for countable, even infinite, disjoint sets. Axiom IV (at least its interpretation in terms of the chain rule) follows from Kolmorogov’s first three axioms. Reichenbach requires it as an additional axiom, because of his mixture of logical and mathematical notation. Without the additional fourth axiom, Reichenbach could not switch between logical conjunction and mathematical multiplication.
Reichenbach proceeds to show that finite frequencies satisfy his four axioms. He construes all probabilities as frequencies of sub-series in a larger series—or what is the same thing for finite sets, cardinalities of subsets in a universal set. Hence his probabilities are always with respect to a non-empty reference class, so the probability that an event is in a class B is in Reichenbach’s notation, P(A, B) where A is the reference class—similar to the modern notation of the conditional probability P(B | A). But the probability logic axioms are so weak that many formal structures satisfy them, and Reichenbach’s claim is a long way from a representation theorem. He fails to provide the additional constraints on the space that probabilities are applied to, which in Kolmogorov’s case are given by the assumption that the space is a sigma-field, i.e. a field closed under complementation and countable union.
Reichenbach’s official definition of probability for infinite sequence pairs ⟨xi, yi⟩ with xi in A, and yi in B, for which the limit p of the relative frequency of B in A exists, is as follows: “the limit p is called the probability from A to B within the sequence pair.” (1949f, p. 69). Constraints on the nature of the sequences are added later (1949f, section 30) that are aimed to formalize aspects of randomness. Probabilities of single cases are “fictive” or elliptical, to be understood as claims about the frequency of a kind of case in an implicit reference class. Elsewhere, Reichenbach puts more emphasis on finite frequencies and even suggests that limiting frequencies are simply a mathematical device for justifying inductive procedures (‘A letter to B. Russell’, 1978, vol. II, p. 405–406). Once introduced, the logical framework is dropped in the mathematical development of probability theory in the book.
In combination with the representation of probability relations by claims in a quasilogical language, the limiting frequency interpretation creates fundamental formal problems that Reichenbach did not foresee. Sets of limiting relative frequencies are not closed under finite intersection; they are not closed under countable union; they do not satisfy countable additivity. They do not, in other words, form a sigma field, or a Borel field, or even a field. (See the entries on interpretations of probability, the early development of set theory, and set theory.) These and several other mathematical difficulties of Reichenbach’s setup are described in van Fraassen (1979).[4]
Reichenbach imposes two further axioms—the axioms of order (1949f, p. 137)—that are supposed to hold necessarily of limiting frequencies for infinite time series. One is trivial, essentially asserting that a conditional frequency on lags (Reichenbach’s term for lags is “phases”) of a constant “variable” can always be replaced by a conditional frequency on no lag of that variable. The second, however, appears to be a very strong stationarity principle that is not generally true: the probability of one variable conditional on a specified common lag of other variables is invariant under all uniform translations of the lags. This axiom seems to derive directly from Reichenbach’s interpretation of the foundations of probability, in particular from Reichenbach’s assumption about normal sequences, described below.
In addition to an axiomatization, Reichenbach attempts to provide a foundation for probability claims in terms of properties of sequences, similar to von Mises. Reichenbach regarded von Mises attempt (von Mises 1919) at formally characterizing a “random sequence” as a failure and instead attempted to characterize a weaker sequence property—a “normal” sequence. In his account of normal sequences Reichenbach retains (although the second only in a weaker form) two features that are deemed essential for random sequences: the lack of “after-effect” and the invariance of the limiting relative frequency under subsequence selection. Informally, the “invariance under subsequence selection” is supposed to capture the idea that the probabilities of events in any infinite subsequence selected from the original sequence by a procedure based on the indices of events in the original sequence alone will be the same as the probabilities of events in the original sequence. “The lack of aftereffect” is supposed to capture the idea that given any initial segment of a sequence, one cannot predict the probability of the next event any better than predicting it based on the limiting relative frequency of events in the infinite sequence. Reichenbach’s definition of lack of aftereffect is not based on initial segments of sequences, but rather on subsequences selected by a particular set of rules (1949f, p. 142). Reichenbach defines a “selection” S as any rule that determines for each member of a sequence whether it is a member of S (p. 143). He intends by a “rule” literally any subsequence.
We are unable to reconstruct exactly what Reichenbach may have intended, in particular since his definition of lack of aftereffect is difficult to distinguish from the criterion of invariance under subsequence selection. But we believe it is something close to the following: A sequence of Bi is “free from aftereffect” if (i) a subsequence is selected based on a rule of the form “For each index i in the sequence, include the (i+k)th element in the sequence if the ith element is B (or ~B),” (ii) if the subsequence thus selected has the same event probabilities as the original sequence, and (iii) if this holds for all lags k > 0. If our reconstruction is correct, this would distinguish Reichenbach’s account of lack of aftereffect from that of invariance under subsequence selection, because the former includes subsequence selection rules that depend on the values of certain items in the sequence, while the latter includes only rules that are based on the indices. Two more definitions are required for the full picture. First, a selection S of a subsequence of sequence A belongs to the “domain of invariance” of B, if the probability of B (for all lags) in S is unchanged from the probability of B in A, and if the same holds for any selection S from A with a lag. Second, a subsequence selected by an algebraic rule that partitions the sequence A—e.g. take every fourth element (see p. 144 for details)—is called a “regular division” of A. Putting the pieces together, Reichenbach requires for the “normality” of a sequence A that it be free of aftereffect and that all “regular divisions” of A are in the domain of invariance of B. This condition of regular divisions seems to underlie the stationarity expressed in the second axiom of order.
If random sequences are taken to satisfy (at least) the conditions of the lack of aftereffect and invariance of subsequence selection under any selection rule, then Reichenbach’s restriction of subsequence selection rules to regular divisions implies that the set of normal sequences is a proper superset of that of random sequences. Reichenbach accepts this weakening to avoid some of the difficulties in characterizing a random sequence, and to broaden his earlier notions of probability to include sequences of trials, which might not be perfectly independent. In later writings, he seems to suggest that as long as the sequence converges, probability claims can be applied to the component events.
A large section of the book is devoted to reconstructing classical results in the theory of probability as claims about relative frequencies, including various continuous distributions and Bernoulli’s theorem. Reichenbach claims that probabilities on continuous domains are “isomorphic” to limiting relative frequencies, but, as van Fraassen (1979) notes, it is difficult to see any sense in which that is true. The remainder of the book is not about probability per se, but about its epistemological role.
Further Reading. A detailed attempt at the reconstruction of Reichenbach’s account of probability and its epistemological grounding can be found in Eberhardt & Glymour (2011), which includes specific references to the original sources.
3. Epistemology and Metaphysics
3.1 Early Views
Reichenbach began his philosophical career as a neo-Kantian, a perspective that is evident in his thesis and in his first book-length effort (1920f) after his doctoral thesis, and that at least echoes in his later work. The aim of The Theory of Relativity and A Priori Knowledge is to reconcile Kantian theory in a limited way with the theory of relativity by distinguishing two senses of synthetic a priori: Principles governing the content of experience can be synthetic a priori because they are necessary, transcendental truths, or because they are non-empirical principles that form part of how we construct our representation of reality, and are thus revisable. Reichenbach endorses the latter constitutive sense of the synthetic a priori, and sees his task as scrutinizing Kant’s principles in light of the “new” reality described in the theory of relativity. Reichenbach’s—never clearly specified—process of a construction of a representation is hidden behind the idea of “coordination”. Particular principles, such as those of causality or probability, are supposed to establish a correspondence between something in experience and our representation of it in the form of a mathematically axiomatized scientific theory (à la Hilbert). What that something is, Reichenbach never clearly describes. He explicitly rejects the proposal that it is just sensation, and he admits that what he is describing is a curious case of “the coordination of two sets, of which one [...set’s] elements are first defined through the coordination” (p. 40, 1965a). While a priori in the constitutive sense, the coordination principles are contingent, they could be changed if experience makes others more convenient. The picture is very much like that C.I. Lewis offers at about the same time in Mind and the World Order (1929).
Reichenbach’s account of the ascension from sense data to individual things to scientific theories is via an account of testing, in spirit close to ideas that Hermann Weyl (1927) and Rudolf Carnap (1936) were later to advance, in which various hypotheses support one another, each functioning as an auxiliary in tests of others, an idea Glymour (1980) later unsuccessfully tried to formalize as “bootstrapping.” The foundational character of sense data and the view that objects and their properties and relations are constructions endures for some years in Reichenbach’s thought, for example in his 1929 essay on “The Aims and Methods of Physical Knowledge” (1929g), where, however, the example and authority is no longer Kant’s first Critique but rather Russell’s Our Knowledge of the External World (1914) and Carnap’s The Logical Structure of the World (1928).
By the late 1920s Reichenbach was moving away from neo-Kantian positions and towards logical positivist views, allying himself with the Vienna Circle philosophers, although he always maintained and emphasized in retrospect that the “empiricist philosophy” he pursued in the Berlin Group was much more focused and engaged with science and did not fall prey to the positivist problems that came out of attempts to ground knowledge on sense data alone. He did not view his contemporaries uniformly. For Moritz Schlick, Reichenbach seems to have had a somewhat condescending respect, for Ludwig Wittgenstein, who is one of the few philosophers whom he later criticizes by name in Experience and Prediction (1938c), and for Karl Popper, none whatsoever. Aside from Einstein, his deepest respect and closest intellectual alliances seem to have been with Kurt Lewin, Kurt Grelling, Rudolf Carnap, Richard von Mises (although they do not seem to have got along personally) and Bertrand Russell, although Reichenbach was not pleased with Russell’s criticism of his views in Russell’s last philosophical book, Human Knowledge, Its Scope and Limits (Russell, 1948; see Reichenbach 1978, vol. II, p. 405).
Further Reading. Chapter 2 of Ryckman (2005) provides a very clear attempt at reconstructing Reichenbach’s struggle with Kantian principles in the 1920s. Padovani (2008) provides a wealth of textual detail and references for the same period, with a more focused notion of Reichenbach’s notion of “coordination” in Padovani (2011, 2015, 2017). Chapter 6 of Milmed (1961) traces the Kantian elements in Reichenbach’s epistemology and discusses the conflicts that arise, though the analysis concerns primarily Reichenbach’s mature views.
3.2 Mature Views: Experience and Prediction (1938)
By the 1930s Reichenbach abandoned foundationalism altogether and adopted an epistemological position closer to pragmatism than to logical positivism. Reichenbach’s mature viewpoint, presented in Experience and Prediction (1938c) diminishes the status of the given; knowledge, belief and conjecture is built around his conceptions of meaning, probability and convention. Coordination of language and physical circumstances replaces his earlier coordination of Kantian concepts and sensation. Reichenbach is a realist about the external world, but asserts that we can only have uncertain knowledge about it, inferred from sense data. Deliberation can reject the gifts of perception so involuntarily received. Claims about ordinary objects, and scientific claims about other kinds of objects, whether sense data or atoms, are probabilistic in nature and related by probabilities, not by any kind of logical reduction. Reichenbach was not alone in this view at the time. In 1935, in the second issue of Analysis, Hempel, writing in English because Carnap could not at the time, described Carnap’s viewpoint in similar, if not quite identical, antifoundationalist terms.
The overall account seems to be something like the following: Language requires a coordination of words—or at least sentences—with something signified. Scientific language, Reichenbach claims, requires “coordinative definitions” that specify physical procedures for measurement. A common example is the “definition” of the Paris meter bar as a unit of distance. Definitions in the usual sense occur within a language, but Reichenbach sometimes appears to intend something like an “ostensive” definition (he does not use the term). He gives no account of how such an act can suffice to specify a rule, and he recognizes instances in which it does not, for example that a coordination that measures time by the behavior of clocks does not suffice to provide a rule for deciding relations of time measurements between distant clocks. Various coordinative definitions may thus leave measures of other quantities or relations indeterminate, and these must be specified by some stipulation or other. His chief, but not only, example is the definition of simultaneity (see also Rynasiewicz (2003), and Dieks (2009) for a clear discussion).
Once specifications of all relevant quantities are made, empirical claims are possible. There are, in Reichenbach’s view, two related ambiguities. First, different stipulations about measurement can lead to apparently different empirical generalizations that nevertheless are empirically indistinguishable—although just what “empirically indistinguishable” can consistently mean for Reichenbach is problematic for reasons to be noted. Second, the same total theory may be partitioned in more than one way into claims true by stipulation and empirical claims. Reichenbach’s solution to these forms of underdetermination is that “equivalent theories” say the same thing. The equivalence relation he intends is unclear. In earlier writings he suggests that empirically equivalent theories are those that have the same empirically testable consequences; a later formulation is that empirically equivalent theories are those that have the same (posterior) probability on any observations. The later characterization is as clear as Reichenbach’s characterization of the probability of theories and their confirmation (see below). The earlier characterization results in a semantics for which no effective proof theory is possible (Glymour, 1970).
One puzzle about Reichenbach’s view of conventions is why characterizing them remained important to him, since they are, in his mature view, only a feature of the reconstruction of a theory, not an intrinsic logical or semantical feature of any proposition. In principle, separating out different presentations of the same theory and recognizing equivalence amid diverse conventions might be of value, but except in cases such as simultaneity and gravitational theories with extra “absolute forces,” Reichenbach did not use reconstruction to that effect, and the most important question of equivalence in the physics of his era, the relation of wave and matrix mechanics, was solved in a quite different way by John von Neumann (1932). Reichenbach’s emphasis on locating conventions seems instead to be negatively motivated, a continuing prophylactic against claims that various principles are a priori.
The immediate description of the perceptual world is in terms of enduring objects, their properties and relationships, and that description is only probable. The world can be described egocentrically in terms of “impressions” and “sense data,” but, Reichenbach argues, ordinary descriptions of things are not equivalent to egocentric descriptions in terms of impressions, because, however elaborate, egocentric formulations do not entail object claims, they only confer a probability on object descriptions, (and, of course, in parallel, given Reichenbach’s anti-foundationalism, egocentric descriptions are only probable). The argument is not in accord with Reichenbach’s own criterion for equivalent descriptions, but the conclusion is repeatedly emphasized. Reichenbach insists, sometimes in rather sharp language, that the logical positivists and unnamed “pretentious” logicians are simply wrong about locating the foundations of knowledge in sense data or analytical truths.
Reichenbach’s mature views on the notion of analytic truth were complex. He no longer held with C.I. Lewis that there is at any time any sort of Kantian a priori—but there is synonymy, there are equivalent descriptions, and the assertion of equivalence between equivalent descriptions is presumably a purely logical matter, hence analytic. Although explicitly addressed to Carnap, C. I. Lewis was quite possibly an equal target of Quine’s “Two Dogmas of Empiricism” (1951). (As Quine’s senior at Harvard, Lewis was unlikely to be criticized by name.) In a brief essay on “Logical Positivism” in 1945, Russell gently but pointedly ridiculed Carnap’s disposition to resolve every apparently irresolvable dispute by appeal to linguistic relativism. Russell’s criticism, and Nelson Goodman’s criticism of the very idea of synonymy (Goodman, 1949), but perhaps not Quine’s, could have been applied to Reichenbach.
All empirical claims are, according to Reichenbach, probabilistic judgments based on relative frequencies in a reference class, or reached by induction. To the extent that reference classes rely on kinds, Reichenbach resorts to psychology: primarily, things are sorted into kinds by the immediate perception of similarity, or by similarity in memory. Less primitively, theory and convention guide the determination of kinds. In practice he recommends the choice of the narrowest reference class for which there are adequate statistics, a recommendation that is of no help (why, or why not, should we throw various astrological theories into the reference class for assessing the prior probability of general relativity?).
Primary or fundamental inductive inference consists of taking observed relative frequencies as probabilities, that is, as limiting relative frequencies. This procedure, referred to as the “straight rule”, implies that one should take the current empirical distribution to resemble the limiting distribution, and therefore behave accordingly. The justification of such taking, or “positing” in Reichenbach’s terminology, is that if there is a limiting relative frequency to a sequence, this procedure will converge to it. Reichenbach notes in The Theory of Probability (1949f) that without further assumptions nothing can be said about rates of convergence or about the warranted confidence that an empirical distribution has converged. He further acknowledges that any procedure that estimates the probability to be the relative frequency, plus any quantity that keeps the estimate between 0 and 1 and that itself converges to 0, will also converge to the limiting frequency if such exists. He there (misleadingly) treats such alternative inductive rules as producing “equivalent descriptions” to the straight rule and takes the choice as of no consequence—but of course the equivalence is only in the limit. In Experience and Prediction (1938c) he instead dismisses such alternative rules on the vague grounds that they are “riskier” than the straight rule.
The proposal of the straight rule goes back to the problem of assertability of probability claims he discussed in his thesis. Reichenbach’s proposal is reminiscent of the law of large numbers, that the empirical distribution of a sequence of independent and identically distributed trials converges in probability to the true distribution. But the law of large numbers depends on independent, identically distributed trials. Reichenbach cannot resort to such assumptions if he wants to avoid circularity in his account of inductive inference. Instead he introduces “posits” that can basically be understood as leaps of (tentative) faith that the empirical distribution is representative. Posits can be “blind” or “appraised.” Posits are blind when there is no data available to justify the posit. For example, if all one has is a sequence of measurements for which the empirical frequency distribution of events is given by F, then a blind posit might state that the probabilities specified by F are within ε, for some small ε, of the true distribution P. One has no reason to justify this claim, the posit is blind. However, if one had several sequences of measurements resulting in empirical frequency distributions F1,…, Fn, then the relative frequencies found in each of these empirical distributions can, according to Reichenbach, be used to get higher order distributional information about the original posit itself, and the posit therefore becomes appraised. So, if one has sequences of measurements of the gravitational constant from the Earth, the Moon, the 7 other planets, and, say, the Cavendish balance—10 sequences in total—and in all cases except for Mercury, the gravitational constant is within some small value ε of g, then the higher order probability of the posit that the true value of the gravitational constant is within ε of g is 9/10. How sure can one be that the appraisal of the posit is accurate?—For that Reichenbach introduces again an even higher order blind posit. One thus arrives at a hierarchy of posits, of which the lower levels are appraised posits, and the highest levels are blind posits. Just how the integration of different levels is supposed to occur, remains unclear and a point of criticism by Ernest Nagel (see below). The general idea appears to be that at the “data” level one counts frequencies and integrates higher levels using Bayes rule.
The approach of estimating higher order distributional information on the basis of subdividing the available sample is similar to the modern statistical procedure of bootstrapping, although there re-sampling techniques are used. Reichenbach argues that his procedure ensures more efficient convergence than does naïve application of the straight rule alone. Faster convergence of the first level estimate—the data-level—is somehow supposed to result from simultaneous convergence at all the different levels in this hierarchy of appraised posits—Reichenbach refers to this as the method of cross-induction. But Creary (1969, Ch. 5) points out that there is no reading of such a conclusion about efficient convergence that follows from the premises Reichenbach assumes.
Over time and place, the reasons Reichenbach gives for convergence of frequency estimates to a limiting value vary, including 1) his early view that convergence is synthetic a priori, or that 2) the principle of induction expresses a kind of psychological habit, 3) the semantic argument we quoted above in Section 2.2 that the negation of the principle of induction is meaningless, 4) a pragmatic vindication that induction using the straight rule works if any method of induction works, 5) a convergence argument based on higher order probabilities, or 6) that there is no guarantee, merely “posits.”
The probability associated with any foundational claim must be understood as a blind posit, i.e. as a good guess, which according to Reichenbach can take into account pragmatic considerations. Thus, Reichenbach posits the existence of the external world as he thought it would make causal laws more “homogenous” (1938c). In a rather mixed metaphor, Reichenbach compares our knowledge of the external world to seeing shadows of flying birds on the walls of a cube in which one is confined. He argues that the patterns on the walls, their regularity, would result in a high probability that there are objects outside the cube producing the shadows.
Reichenbach’s eventual anti-foundationalism led him to a contest of opinions with C.I. Lewis, whose accounts of empirical learning and reasoning in Mind and the World Order (1929), and in An Analysis of Knowledge and Valuation (1946) rested on a phenomenalist foundation of “qualia” (see the entry on qualia). Lewis, like Reichenbach a probabilist at heart, insisted that the assessment and revision of probabilities in the light of experience requires that some propositions obtained from experience be certain, or as he put it, “if anything is probable, something must be certain.” Reichenbach denied the claim, arguing that the deliverances of experience directly provide, not certainty for claims about qualia, but only probabilities for claims about ordinary things. Those probabilities can be revised in the light of further experience. For the same reason, in his unremittingly critical review of Karl Popper’s The Logic of Scientific Discovery (Popper 1935), Reichenbach argues that probability assessments are essential in the “falsification” of theories (1935e, 1978, vol. 2, p. 372). Lewis’ actual complaint appears to be based on a mathematical error when computing conditional probabilities. Reichenbach pointed out Lewis’ error, but did not provide a positive example to refute Lewis’ concern (Peijnenburg & Atkinson, 2011). A more general problem that appears to have been missed in the discussion at the time is that since Reichenbach held that the probabilities of theories are to be assessed by Bayes rule, his position, unlike Lewis’, required a technical account of how claims with non-extremal probabilities can produce changes in the probabilities of others by some generalization of Bayes rule (see the entry on Bayes Theorem). Since on Reichenbach’s view uncertainty is associated with observation and perception and scientific theories are only confirmed with a degree of probability, an account is required of how uncertain data changes the probabilities of hypotheses logically remote from the data. Much later, Richard Jeffrey (1983) provided an account of Bayesian updating that explicitly relates the probability of the data to the probability of the hypothesis confirmed—or disconfirmed—by the data (see the entry on Bayesian epistemology).
Bayes rule and the probabilities of theories posed another problem pressed on Reichenbach by Ernest Nagel in a review in Mind of the German edition of Reichenbach’s The Theory of Probability (Nagel, 1936; see also Nagel, 1938). Nagel’s courteous review found a series of difficulties with Reichenbach’s theory, beginning with the logical status of the “probability implication” which Nagel thought was not, contrary to Reichenbach, of the same kind as material implication, because Reichenbach’s relation is not “extensional.” Nagel does not explain what he means, and Reichenbach’s extended response in 1939 does not clarify the matter (1939b, 1978, vol. 2, p. 388). In his response to Popper (1935e), Reichenbach had proposed two ways of evaluating theories, one of which is to count the relative frequency of true statements among the consequences of a theory. Nagel points out that a theory 10% of whose tested predictions are false would scarcely have probability 0.9. Reichenbach does not attempt to defend this proposal in his reply to Nagel in 1938 (Reichenbach, 1938a). That leaves the assignment of probabilities to theories by Bayes Rule, which Reichenbach had also proposed, but Nagel observes that if theories are to be evaluated by Bayes rule they must have prior probabilities. How can there be a frequentist prior probability for a theory, since we do not know to what reference class to assign a particular theory and, whatever the reference class, according to Reichenbach we do not and cannot know which theories in that class are true? As in several of his other responses to criticism, Reichenbach’s 1938 reply is unfortunately more defensive than enlightening. About the reference class, Reichenbach says only “I do not think this is a serious difficulty as the same question occurs for the determination of the probability of single events” and recommends the choice of the narrowest reference class for which there are adequate statistics (though how the adequacy of a statistic for the truth or falsity of theories is assessed is never explained). Reichenbach gave a sketch of such a procedure in his 1935 reply to Popper, which Nagel pointedly does not think addresses the problems. About the problem of the frequency of true hypotheses in the reference class, Reichenbach says that we only need the probabilities of theories in the reference class, not their truth or falsity—a question-begging reply that Reichenbach must have sensed is unconvincing because he promises to address the issue further in Experience and Prediction (1938c). The discussion of the prior probabilities of theories in section 43 of Experience and Prediction is unsatisfactory for the same reasons.
Reichenbach’s most enduring distinction is between “the context of discovery and the context of justification.” But Reichenbach did not always allow the distinction, and the distinction he intended is not quite the one commonly attributed to him. In his 1922 essay on “The Philosophical Significance of the Theory of Relativity” (1922c) the (now conventional) distinction between the context of discovery and the context of justification is formulated in other terms, and rejected:
It is important to follow the concepts by which the theory finds its way step by step and to level criticisms at the theory from the same intellectual path as was used in the creation of the theory. This work derives from such an attitude; indeed to renounce this method would achieve nothing but to promote traditional representations to a status of absolute predominance. (Reichenbach, 2006, p. 97.)
In his review (Reichenbach, 1935e) of Popper’s The Logic of Scientific Discovery, Reichenbach suggests that theories are ordered by their prior probability, and the theory with the highest prior is further tested. In Experience and Prediction (1938c) and in his reply to Nagel (Reichenbach, 1938a), published in the same year, Reichenbach first formulates the distinction between the context of discovery and the context of justification with regard to mathematics: the mathematical relations are what they are, and how we come to recognize them is an entirely different, psychological matter:
The objective relation from the given entities to the solution, and the subjective way of finding it, are clearly separated for problems of a deductive character; we must learn to make the same distinction for the problem of the inductive relation from facts to theories. (1938a, p. 36– 37)
In other words, the distinction is supposed to be between objective relations among premises and conclusions, and subjective ways of discovering those relations. The “context of discovery” is not about search for hypotheses or about the order in which hypotheses are considered but about the search for the objective inductive relation between a theory and a body of evidence. What little Reichenbach had to say publicly about how to search for promising hypotheses was reported in his review of Popper’s book, and in his dismissal in his reply to Nagel of Peirce’s “abduction” as a confusion of mathematical and psychological relations. While Carnap later imagined an inductive, logically omniscient robot (Carnap, 1960), and Hempel much later (in “Thoughts on the Limitations of Discovery by Computer”, Hempel 1985) claimed that computerized generation of interesting scientific hypotheses is impossible, Reichenbach seems not to have given any thought to questions about how to come up with hypotheses and about better and worse ways to search through the space of logically possible theories. He had one fundamental procedure for estimating true hypotheses: the straight rule, and one secondary procedure, whose application he never coherently explained, Bayes rule with objective, frequentist, prior probabilities for hypotheses.
Further Reading. Putnam (1991) provides a helpful big picture of Reichenbach’s mature views on metaphysics and epistemology. Chapter 7 of Milmed (1961) provides an overview of Reichenbach’s probabilistic epistemology and views on induction. Salmon, in various papers (see the entry on the problem of induction) tried in vain to save the straight rule, Reichenbach’s pragmatic vindication of induction (see also Hacking, 1968). Eberhardt & Glymour (2011) try to reconstruct the details of Reichenbach’s probability logic and discuss some of the criticism leveled at Reichenbach’s account in more detail. Psillos (2011) disentangles Reichenbach’s argument for realism. Galavotti (2011) provides a succinct attempt at reconstructing a coherent overall account of Reichenbach’s epistemology. Chapter 6 of Milmed (1961) provides one of the few good discussions of Reichenbach’s views on logic. An entire collection of articles in Schickore & Steinle (2006) explores the different interpretations, historical connections and philosophical offspring of Reichenbach’s distinction of the context of discovery and the context of justification.
4. Philosophy of Physics
Almost exclusively, Reichenbach’s scientific interest was in physics. He regarded chemistry as an appendage, entirely reducible to physics, and his only publication touching the subject is on Marcelin Bertholot (Reichenbach, 1927a), the eminent French anti-vitalist chemist. Of biology, Reichenbach leaves open (at least in 1929) the serious possibility that life exhibits phenomena that cannot be explained by physical laws, and of evolution he remarks that it has disappointed in failing to explain “the problem of life” (1929g, Section 2). He believed Freud’s psychoanalytic theories were scientifically warranted by Freud’s evidence, and in Los Angeles maintained friendships in the psychoanalytic community, including attending and sometimes lecturing at the Psychoanalytic Institute. As a student Reichenbach showed some interest in psychology (Padovani, 2008, p. 13), however, except for brief passages in Experience and Prediction (1938c), Reichenbach published nothing about psychology, and we have no evidence regarding how familiar he was with Freud’s publications. It seems unlikely that Reichenbach knew Freud’s remarkably candid descriptions before 1900 of his aggressive data collection procedures, and of course Freud’s letters to Wilhelm Fleiss (Masson, 1986), which reveal how little Freud thought of his own methodology, were unknown to Reichenbach.
Reichenbach’s most original work on the foundations of physics is in three books, Axiomatization of the Theory of Relativity (1924h), Philosophical Foundations of Quantum Mechanics (1944b), and The Direction of Time (1956b). The first attempts an empiricist aufbau of the special and (in less detail) general theories of relativity from experimentally accessible causal relationships; the second essays a novel 3-valued logic for quantum theory; and the third addresses a long standing problem in physics and metaphysics. The Philosophy of Space and Time (1928h), Reichenbach’s most widely read, most elegant, and least original work on physics, combines an extension to spacetime theories of Helmholtz’s and Poincaré’s conventionalism about geometry with a description of Einstein’s special and general relativity theories from the point of view of the Axiomatization, much of which it repeats.
4.1 The Theory of Relativity and A Priori Knowledge (1920)
Einstein’s lectures on relativity in Berlin in 1917–18, attended at the time by Reichenbach and a handful of others, provided a shock to Reichenbach’s viewpoint. The Theory of Relativity and A Priori Knowledge, published in 1920, is an attempt to identify neo-Kantian doctrines that must be abandoned and to articulate what can be salvaged. Twenty-five years before, in his dissertation published in 1897, Russell had undertaken a similar project in connection with non-Euclidean geometry, arguing that constant curvature is the geometrical synthetic a priori. In 1902, Poincaré’s Science and Hypothesis essentially supplemented Russell’s view with the opinion that the choice of constant curvature geometry is underdetermined; the choice of one such geometry rather than another can always be compensated by a change of physics to save the phenomena. Without mentioning Russell or Helmholtz, Reichenbach takes general relativity to have refuted both Poincaré’s geometrical conventionalism and Kant’s geometrical apriorism. Most of the book addresses general epistemological issues discussed above rather than issues about physics per se.
4.2 Early Writing on Relativity
Between the publication of The Theory of Relativity and A Priori Knowledge, in 1920, and the appearance of The Axiomatization of the Theory of Relativity in 1924, Reichenbach published a series of professional and popular essays expounding or defending the special and general theories and Reichenbach’s own axiomatization, which was published in outline in 1921 in Physikalische Zeitschrift (1921d). The professional essays were variously addressed to audiences of philosophers or physicists. They are interesting for our purposes chiefly because they state philosophical positions that Reichenbach had previously rejected, or would later come to reject, or because they offer interpretations of the theories that are problematic. Notable in the last respect is Reichenbach’s view that general covariance is a substantive claim of general relativity: the laws of physics have the same “form” in every coordinate system and frame of reference. Reichenbach does not explain the idea of the “form” of a physical law.
While Kantian perspectives—the a priori “constitution of the object”—still linger, the “Philosophical Significance of the Theory of Relativity”, published in French in 1922, signals a break with some of Reichenbach’s previous views (1922c). Perhaps influenced by Einstein’s “Geometry and Experience” (1921) Reichenbach no longer holds that, contrary to the conventionalist views he attributes to Helmholtz and Poincaré, the theory of relativity has established a geometry as part of physics to which there can be no empirically adequate alternative. After introducing the idea of a universal force affecting all objects no matter how insulated, and noting that gravitation as usually conceived is such a force, Reichenbach writes that: “The solution to the problem of space is…found only in this conception we call conventionalism…which goes back to Helmholtz and Poincaré.” (Reichenbach, 2006, p. 135). The idea that empirically indistinguishable hypotheses differ only verbally—“equivalent descriptions” in Reichenbach’s terminology—is already developed here.
4.3 Axiomatization of the Theory of Relativity (1924)
In 1921 Reichenbach published a very limited précis of the approach to the theory of relativity he ultimately presented in 1924 (Reichenbach, 1921d). The Axiomatization is either a work very much out of its time, or the times have not changed much. Reichenbach’s statement of purpose might have been written at any time in the last quarter of the 20th century in response to Quine’s holism and to Thomas Kuhn’s incommensurability thesis (see the entries on belief and on Thomas Kuhn).
It is not easy to arrive at…a judgment with respect to the axioms of a theory. Usually the axioms, representing higher levels of abstraction, are quite remote from direct sense perception…
In order to avoid this difficulty…It is possible to start with the observable facts and to end with the abstract conceptualization…The empirical character of the axioms [about observables] is immediately evident and it is easy to see what consequences follow from their respective confirmations or disconfirmations.
Unfortunately…every factual statement, even the simplest one, contains more than an immediate perceptual experience: it is already an interpretation and therefore itself a theory…The most elementary factual statements, therefore, contain some measure of theory….
Does there exist any confirmation other than that of the theory as a whole? …Let us assume that the theory by means of which we explain a certain fact is false and is to be replaced by a different one. It is nevertheless possible that the new theory, when used for the interpretation of this one fact, makes hardly any difference quantitatively, whereas it leads to considerable changes with respect to other assertions…
The new theory has merely to satisfy the requirement that it will not result in a practically noticeable quantitative difference when applied to these elementary facts…For this reason all axioms of our presentation have been chosen in such a way that they can be derived from the experiments by means of pre-relativistic optics and mechanics. All are facts that can be tested without the use of the theory of relativity…The particular factual statements of the theory of relativity can all be grasped by means of pre-relativistic conceptions; only their combination within the conceptual system is new. (p. 5–7)
The book is divided into two parts, one on special relativity and the other on general relativity, each in some respects dependent on the other. The first part presents a series of postulates about the behavior of light, accompanied by a series of definitions. The primitives are a directed acyclic graph whose vertices are point events and whose edges represent the relation “a signal can be sent from event A and received at point B,” and a partitioning of the event space by assignment of each event to a point on some real line—intuitively, a world line—such that the set of events assigned to the same line are equicardinal with the line and their ordering by signaling is the ordering of the real line, and such that no two such world lines intersect. Axioms about the behavior of signals, especially “first signals”—meaning light signals—are intended to specify sufficient constraints so that the coordination determines an inertial frame of reference in Minkowski space-time. Extensive discussion is given over to the impossibility of experimentally determining a “metrical” simultaneity relation—that is, of finding experimentally a unique simultaneity 3-space for an inertially moving observer. “Matter axioms” are then added specifying transport properties of rigid rods and the connection of rigid rod distance measurements with round trip time measurements (although one of the “matter axioms,” Axiom VI.2, is entirely about clock transport). Reichenbach asserts that the four matter axioms that are restricted to inertial frames follow from his light axioms. That is not true, and 60 pages later Reichenbach qualifies the claim to mean only that the relations follow from the general theory of relativity.
Reichenbach very briefly discusses the classical tests of the general theory of relativity: the red shift of light emitted from the sun, the bending of starlight passing near the limb of the sun, and the anomalous advance of the perihelion of Mercury. He summarizes: “…only the deflection of light and the red shift can furnish evidence for Einstein’s relation between gravitation and the real metric…” (p. 170). A far more enlightening analysis of the bearing of the classical tests had been given by Harold Jeffreys in 1919 and taken over (without acknowledgement) by Arthur Eddington in The Mathematical Theory of Relativity (Eddington, 1924); Jeffreys’s approach eventually led to the modern parameterization of metrical theories of gravitation.
The Axiomatization has three difficulties. It contains a mathematical error discovered by John von Neumann in the proof that two frames of reference satisfying his five light postulates and definitions could not have a world line at rest in common. Reichenbach acknowledged the error in 1925, and again in 1928, without proposing any modification to obtain uniqueness. In an unflattering review, Herman Weyl gave a second reason (Weyl, 1924; see also Rynasiewicz, 2005): the light cone structure of Minkowski space time does not suffice to specify a unique set of inertial frames unaccelerated with respect to one another, and hence neither do Reichenbach’s axioms. By introducing a singularity in the infinite past, a system of accelerated frames can be used. Weyl took this fact to defeat the very purpose of Reichenbach’s attempted reconstruction of the theories: to found them on observable relationships. But perhaps the most important problem is that much of Reichenbach’s construction, without the philosophical commentary, had been anticipated by A.A. Robb, first in 1914 (A Theory of Time and Space), and then in 1921 (The Absolute Relations of Time and Space) for both special and general relativity. Reichenbach does not mention Robb in 1924 or, to our knowledge, later, even though Robb’s 1921 book was reissued with a different title in 1936.
Reichenbach’s apparent unfamiliarity at the time with the English language literature on relativity is notable and unfortunate. He cites only one essentially English language source, from The American Journal of Mathematics, and seems not to know of the work of Jeffreys or Robb. He does appear to have read Eddington’s 1921 paper on Weyl’s theory. Whatever the cause, the Axiomatization, which is one of Reichenbach’s most original technical efforts, would have been a different work, or none at all, had he taken account of those developments.
Further Reading. Section 4.4 of Ryckman (2005) provides a more detailed analysis of what Reichenbach was trying to do in this book. Dieks (2020) contrasts Reichenbach’s and Weyl’s foundations of space and time.
4.4 The Philosophy of Space and Time (1928)
Published only 4 years after the Axiomatization, The Philosophy of Space and Time (1928h) is an engaging unification of a multitude of ideas Reichenbach had previously published, including the distinction between descriptive and inductive simplicity, the synonymy of “equivalent descriptions,” the distinction between differential and universal forces, the necessity of coordinating definitions and their “conventionality,” the conventionality of spatial metrics and of “metrical” simultaneity, and the account of the logical structure of relativity theories in terms of properties of causal relations in the Axiomatization.
The introduction to The Philosophy of Space and Time betrays the Marxist inclinations Reichenbach retained from his student years. Science he says, has become mechanized, and develops so rapidly and automatically that its practitioners cannot reflect on what they are doing or why. (He might as well have said they are “alienated from their labor,” but he did not.) A philosophical counterweight (he might as well have said “antithesis,” but he did not) is needed. The counterweight cannot be provided by individuals announcing philosophical manifestos; it requires that philosophers organize into groups so that, collectively, they can keep up with, and exercise analytic control over, the products of the scientific machine. The Vienna Circle, and Reichenbach’s own group of philosophers and physicists in Berlin, are the models. Together, philosophers should produce results, not manifestos. This last demand was the conclusion of the editorial Reichenbach placed in the first issue of Erkenntnis in 1930 (Reichenbach, 1930a); Schlick and Carnap, his collaborators in founding the journal, refused to sign the editorial, Schlick resigned entirely as an editor.
The book begins with a clear and compelling discussion of the interdependence of properties and laws, illustrated through the relations of alternative measures of length and alternative geometries. The examples are then used to make two general claims, first that within the structure of complex theories there are identifiable points that are definitions, and, second, that alternative systems of definitions and laws that account for the same “facts” say the same thing, have the same content. Reichenbach’s “definitions” are not purely verbal, they are “coordinative definitions” that specify physical procedures for determining the values of quantities. The point is reinforced with a distinction between differential and universal forces. Universal forces influence all objects in the same way (where theory specifies what a “way” is) and cannot be shielded against. Heat, for example, is a differential force because it affects bodies of different compositions differently, whereas gravity is a universal force. A space with curvature can be equally described as a space without curvature but with a universal force. Without explicit statement, Reichenbach takes for granted the view, later defended in Experience and Prediction (1938c), that talk in coordinative definitions about ordinary, middle-sized, nearby physical objects and processes is intelligible and legitimate.
Reichenbach has a complex discussion of visualization. He introduces Helmholtz’s idea that to visualize a geometry is to understand what experiences one would have in a world in which that geometry holds, and extends the idea to the visualization of spaces with compact topologies, where, Reichenbach argues, Euclidean geometry could be sustained but at the cost of causal anomalies. For example, in a toroidal space, travel on a geodesic would bring one back to one’s starting point, which, Reichenbach argues, would require either abandoning Euclid or else allowing “causal anomalies” in the form of duplicate worlds at regular distances from one another. (By “Euclidean” geometry, Reichenbach means here a geometry on a manifold homeomorphic to R3, since there is a complete Euclidean metric for toroidal 3-space.) Reichenbach gives other examples of causal anomalies but no general characterization.
Even with Helmholtz available, Reichenbach is concerned to dispute further the very idea that Euclidean geometry has a privileged status in mathematical visualization that indicates some intrinsic limitation of thought. If humans had somehow been transported to a non-Euclidean world, he says, they would have non-Euclidean visualizations—surely a puzzling counterfactual. The very idea that “pure visualization” has some normative content is a mistake, he argues: “the normative function of visualization is not of visual but of logical origin.” (p. 91). We do not presume to know just what Reichenbach meant here, but for a plausible elucidation one might turn to recent philosophical work on the logical relations implicit in geometrical diagrams.
Reichenbach’s discussion of space and time begins with a near irony. Having argued against Kant’s effort to justify the basics of Newtonian physics a priori, Reichenbach proceeds to argue that we can know almost a priori that Newtonian theory is false. For example, Newton does not distinguish between the length of a moving segment and its length at rest, but according to Reichenbach, this is an a priori mistake: “the measurement of a segment with a measuring rod that moves relative to it requires the formulation of a new concept…The length of a moving line-segment is the distance between simultaneous positions of its endpoints.” (p. 155) And further: “It follows from the nature of the extended concept of length that the length of a moving segment is generally different from its rest-length.” To say which is the true length is “nonsense” (p. 157). Thus is Newton refuted.
Most of the rest of the book is a restatement of the Axiomatization with more extended examples and fewer proofs, and explicitly construed as a reduction of space time relations to causal relations supplemented with definitions. The fundamental causal relation to which Reichenbach appeals must be asymmetric and allow reidentification of objects or their features. Reichenbach thinks to obtain the asymmetry via a criterion of causation that invokes both the preservation of something material and the asymmetry of intervention. A “mark” placed at the beginning of a causal process can be received at the end of the process; Reichenbach’s example is the color of a light signal. The asymmetry is that if the beginning of the process is marked, the end of the process bears the mark, but if the end of the process is marked, the beginning does not bear the mark. The analysis thus depends on a distinction between observing a mark and the asymmetric relation of causing a mark. Reichenbach recognizes that for his empiricist, causal construction of the space metric, signals must be reidentifiable, a relation he notes that Kurt Lewin had discussed (in his 1922 Habilitationsschrift) as “genidentity” (see also Padovani (2013)). Unsurprisingly, Reichenbach offers no guide to reidentification, which is obtained in all cases, including those of light signals, from elaborate convictions—or at least habits—about all kinds of details and regularities of the world. Had Reichenbach thought it necessary to his constructions in the Axiomatization first to establish empiricist criteria of genidentity, the construction would not have begun.
Further Reading. Ryckman (2007) gives a more general overview of Reichenbach’s philosophy of physics. Wilholt (2012, pp. 44–48) provides a useful description of Reichenbach’s conventionalism and Giovanelli (2016) discusses in great detail Reichenbach’s early views on the geometrization of physics by general relativity which were at some point supposed to form an appendix to The Philosophy of Space and Time. The collection by Lutz & Tuboly (2021) contains several articles that provide context for Reichenbach’s philosophy of physics.
4.5 Quantum Mechanics and 3-Valued Logic
Reichenbach’s discussion of quantum mechanics contains a (then) standard presentation of the formalism of the theory, including the Born rule and, without stating it, the Projection Postulate (see the entry on quantum mechanics). It is marked, however, by Reichenbach’s empiricism about meaning, by his frequency interpretation of probability, by a three-valued “quantum logic” and by a curious neglect of the major problems and of some the most important previous foundational literature. For later philosophical readers, the missing piece in Reichenbach’s discussion of the theory is the measurement problem (see the section on the measurement problem in the entry on philosophical issues in quantum theory): he gives no account of how the dynamical equation of the theory can account for uncorrelated measurement and object systems becoming correlated in a measurement interaction.
There was a considerable history of “quantum logics” before Reichenbach’s work (see the entry on quantum logic). Martin Strauss had published a theory similar in spirit, but not in detail, to Kochen and Speckers’ partial Boolean algebras (which appeared only thirty years later; see the entry on the Kochen-Specker theorem), characterized by the fact that propositional connectives were allowed only among simultaneously “verifiable” propositions. Reichenbach objects that some quantum mechanical propositions whose logical form contains no propositional operators may be unverifiable. Paulette Fevrier had also introduced a three-valued logic, to which Reichenbach makes a similar objection. Strikingly absent is any reference to Birkhoff and von Neumann’s 1936 paper on the logical structure of quantum mechanics, which introduces a logical structure for orthocomplemented lattices and projective geometries. We can scarcely believe Reichenbach did not know of it and the neglect is difficult to explain. Reichenbach seems to know of everything else, and he was in correspondence with Bargmann at the Institute for Advanced Study. Reichenbach cites von Neumann’s Mathematical Foundations of Quantum Mechanics (1932), but only with regard to von Neumann’s no hidden variable theorem (see the entry on quantum logic and the section on the measurement problem in the entry on philosophical issues in quantum theory).
Reichenbach’s quantum logic has three values, True, Indeterminate, and False. Indeterminate is the value of propositions that quantum theory implies cannot be assessed to be either true or false. Three unary propositional functions are defined, one corresponding to classical negation, as well as seven binary functions, including classical disjunction, conjunction and equivalence.
Reichenbach gives no axiomatization and no rules of inference (although passages suggest he intended an analog of modus ponens to hold for his two new conditional functions) and of course he therefore provides neither soundness nor completeness theorems. Nor does he characterize the class of functions that may be defined by composition of his propositional functions. He does derive various properties of the new connectives from their definitions.
Reichenbach was quite explicit that logic is not empirical. “The rules of logic cannot be affected by physical experience.” (p. 102). His logic with Indeterminate as a value of propositions is the same as logic with “not empirically meaningful” as a value. In Reichenbach’s view that is the logic, as it were, with or without quantum mechanics. It is only that, before quantum mechanics, the principle of equivalent descriptions precluded any need to pay attention to the Indeterminate value.
4.6 The Direction of Time (1956)
As early as 1925, Reichenbach had essayed a probabilistic account of the direction of time (1925d) and in 1931 he still endorsed it, rejecting on familiar reversibility grounds proposals to rely on entropy increase. (1931i, 1978, vol. I, p. 336). His final work, almost completed at his death, was on the direction of time.
Reichenbach did not doubt that we have a definite psychological separation of time into past and future, corresponding respectively to events that can and cannot be remembered. His concern in The Direction of Time is for a physical basis for the same asymmetry:
The problem which the physicist faces can be formulated as follows. The elementary processes of statistical thermodynamics, the motions and collisions of molecules, are supposed to be controlled by the laws of classical mechanics and are therefore reversible, the macroprocesses are irreversible, as we know. How can this irreversibility of macroprocesses be reconciled with the reversibility of microprocesses? (p. 109)
The issues of a specific physical explanation of the psychological asymmetry, and of how there can be a changing psychological present—a moving “now”—were to have been addressed in an unwritten final chapter.
Reichenbach offers three accounts of the direction of time. The first is that the direction of time in a region of space-time is the most common direction of increasing entropy among multiple nearly isolated systems in that region. The idea, as Reichenbach notes, is Boltzmann’s. The second answer is that the direction of time is that in which causal events turn high entropy systems into low entropy, ordered systems. In the reverse direction of the same process, he says, from low entropy to high entropy, the sequence of events is not causal but “purposive.” Thus stepping in sand makes a shape (low entropy) from a flat surface (high entropy). The reverse process, removing the foot from the sand followed by the foot impression filling with sand is not causal, but purposive. We do not pretend to understand this argument. The third argument intends to produce a direction of time from causal directions inferred from macrostatistics. This is the perhaps the aspect of the book most often discussed, and it both breaks new ground and occasionally stumbles in the furrows.
Reichenbach argues that spatially and temporally close coincidences of two causal processes suffice to determine that the coincidence is either a common cause or a common effect of two other events. (He postpones the issue of how it can be known that there is any causal connection between remote events.) He claims, correctly, that this implies that a causally connected network—an acyclic directed graph—of events can have only two orientations; reversing any edge requires reversing all other edges to yield an equivalent directed graph. In an anticipation of 21st century discussions (Woodward, 2003), he considers whether interventions can disambiguate cause from effect in such a network, and argues that they cannot, on counterfactual considerations that are not entirely clear to us.
Reichenbach’s discussion of the relations of probability and causality was begun in his doctoral thesis, and continued in his 1925 paper (Reichenbach 1925d) which, until The Direction of Time, he often cited himself with approval. In The Direction of Time Reichenbach acknowledges that the 1925 claims were incorrect and formulates a new “Principle of the Common Cause” this way: “If an improbable coincidence has occurred, there must exist a common cause” (p. 157). In any instance, he says, the conclusion of the principle is not certain but only probable, the more probable the more frequent the coincidences. He formulates four conditions he says are satisfied when an association of simultaneous occurrences of A and B is due to a common cause, C, simultaneous with neither A nor B: C is not independent of A or of B, but A and B are independent conditional on C and also independent conditional on ~C. He says the principle is sometimes used in a weaker sense, requiring only that the probability of A and of B be raised by the occurrence of C, but he says, that the independence can usually be established “by the use of a more detailed description [of] the cause C” (p. 161, n.2). Reichenbach does not say that his conditions are sufficient for C to be a common cause of A and B, and as Artzenius has noted, they are not (Artzenius 1993 and the entry Reichenbach’s common cause principle).
Using the principle, Reichenbach considers how to distinguish structures I and II below:
Considering only binary variables, Reichenbach says in structure I, the common cause case, A and B are not individually independent of C (the probability of each is greater conditional on C than conditional on ~C), but A and B are independent of one another conditional on C and on ~C. He claims—erroneously—that these facts do not distinguish between I and II, and indeed are typical of causal structures such as II. Using an example with the structure III he writes: “For instance, the spouting of the geysers may have the effect that two clouds are formed which merge into one large cloud. Then the occurrence of this large cloud is an effect E which satisfies [the probability properties of I]” (p. 162). This is an important mistake. In structure III, representing the causal structure of the geyser cloud example, A and B are independent conditional on D, but for almost all probability distributions, A and B are not independent conditional on C and D. That is, III implies (for almost all probability distributions) that none of A, B, C, D are independent, that A, B are independent conditional on D, and that A, B are not independent conditional on C or on C and D. If the directions of edges in III are reversed, as in IV, the same relations hold, but with C and D interchanged. The direction of the causal relations between the eruption and the formation of the large cloud is thus encoded in the conditional probability relations. Reichenbach mangles the relationships in a confused passage:
…if there exists a conjunctive fork with respect to a common effect E [as in structure II, with E in place of C], the simultaneous occurrence of A and B is more probable than a mere chance coincidence. Consequently, if there were no common cause C [D in structure III], the common effect would establish a statistical dependence between A and B and explanation would be given in terms of a “final cause”. …we regard final causes as incompatible with the second law of thermodynamics and consider such forks impossible….this means: The principle of the common cause does not exclude, throughout, a statistical dependence with respect to a common effect; but it does exclude such dependence if there exists no common cause. (p. 162)
Thus Reichenbach seems to think that in II above, A and B are independent conditional on C, but in III, A and B are dependent conditional on C and the absence of D. Reichenbach’s confusions on these points is understandable—well into the 1990s much the same could be heard from several statisticians. In order to see the correct relations, Reichenbach would have had to have explicitly formulated the factorization of the joint distribution for binary variables that is implicit in his other discussions, and computed the joint distribution of independent causes conditional on values of a common effect. He did not. Alternatively, with linear systems it is trivial to calculate the partial correlations of the causes controlling for the effect, but Reichenbach undoubtedly did not know the formulas.
He continues with an illustration of “screening off” and a definition of “causally between” for events. The illustration is a causal chain A → B → C. A and C are independent conditional on the occurrence of B. He does not say that “screening off” requires that A and C are also independent conditional on ~B, but his statement of the Principle of the Common Cause strongly suggests as much. He defines “causally between” as follows:
Definition 1. An event A2 is causally between the events A1 and A3 if the relations hold:
- 1 > P(A2, A3) > P(A1, A3) > P(A3) > 0
- 1 > P(A2, A1) > P(A3, A1) > P(A1) > 0
- P(A1. A2, A3) = P(A2, A3)
(p. 190)
Recall that the dot is conjunction, and P(A2, A3) in Reichenbach’s notation is P(A3 | A2) = P(A3. A2) / P(A2) in the currently conventional notation. Reichenbach goes on to claim that a common effect of two causes is causally between its two causes, thus A1 → A2 ← A3, which is obviously false if absence of any causal connection implies independence. Throughout his life, Reichenbach implicitly makes this assumption in his examples about causal relations. With such an assumption, it follows that P(A1. A3) = P(A1) P(A3) ≥ P(A1, A3) = P(A1)P(A3)/P(A3) = P(A1), contradicting (1) in the definition. One may take these and other examples as evidence that Reichenbach did not have in mind instances of what is now called the causal Markov condition—that conditional on its relatively direct causes a variable is independent of variables that are not its effects—or, alternatively, that he was simply confused about the properties of “colliders”—common effects—in causal graphs. We prefer the latter interpretation.
Causal direction in a network is now determined by supposing an asymmetrical intervention is available, which Reichenbach calls a “mark.” Marks are assumed to be passed down causal chains, and to imply an increase in the probability of each downstream event. Using the time order so obtained, “causal relevance” is defined as:
Definition 2: An event A1 is causally relevant to a later event A3 if P(A1, A3) > P(A3) and there exists no set of events A2(1),…, A2(n) which are earlier than or simultaneous with A1 such that this set screens off A1 from A3. (p. 204)
Definition 2 provides a clear anticipation of a proposal made 20 years later by Patrick Suppes (Suppes, 1970). The Direction of Time ends with a discussion of quantum statistical mechanics focused on issues of the identity of particles through time.
5. Logic and Modality
Reichenbach entertained non-standard logics as early as 1925 in the form of “probability logic.” In the Theory of Probability, probability logic amounts to no more than the assignment of probability values to formulas in the propositional calculus. Later, a three-valued logic was introduced for quantum theory, as discussed above. Reichenbach’s major effort in logic, however, is in Elements of Symbolic Logic, published in 1947, but begun as lecture notes for courses during Reichenbach’s Turkish years. The book is notable chiefly for the extended and detailed effort to formalize universal logical structures of conversational languages within the limits of first order logic and type theory. Reichenbach’s knowledge of German, English, French, and especially, Turkish, helped to make his proposals linguistically serious, and the result, a detailed, and in some respects quite original, logical grammar, including accounts of adverbial modification, tense and modality, is substantially richer than related logical efforts of his contemporaries. Other topics of interest, such as vagueness, are not discussed—Reichenbach perhaps considered vagueness a mistake rather than a topic for logical analysis.
In 1948 Reichenbach circulated an unpublished manuscript (1948e, 1978, vol. 1, p. 409–428), touching on Hilbert’s program and Gödel’s theorems. Reichenbach was not persuaded that Gödel’s proof of the impossibility of proving consistency within a sufficiently strong formalized language was of any philosophical significance.
…a more profound analysis shows Hilbert’s program to be unshaken, and independent of Gödel’s results.
To prove the latter statement first, let us inquire into the significance of the theorem stating that the proof of consistency is only to be given in the metalanguage. What then would happen, if the metalanguage should turn out to be inconsistent? This would lead to the consequence, not that our deduction of the statement of consistency is incorrect, but that the contrary of this statement could also be deduced; and this indeed would make our statement valueless. Now let us assume for a moment that Gödel’s second theorem did not hold, or with other words, that Gödel had proved the contrary of his theorem.
This would mean that the proof of consistency of the language L could be given within L. A simple analysis shows that this would not improve the situation, since in this case our proof of consistency of L would be of value only if we were sure that L is consistent. In case L were not consistent, we could also deduce the statement of the consistency of L, with the qualification that then the negation of the statement were deducible too. Thus if the consistency of L were deduced within L, this fact would not prove the consistency of L. (p. 409–410)
Hilbert’s meta-proof of consistency, by contrast, Reichenbach thinks is genuinely important. The consistency of any “interpreted” formalism can be judged empirically if there is empirical evidence for the claims made within the formalism, and Reichenbach argues that the proposition within the formalism that asserts that the interpreted formal system is consistent has an empirical probability (the only kind Reichenbach allows, of course) at least as high as that of any other claim in the language. But for mathematics, the language must be separated into the part concerned with rational numbers, which can be interpreted so that measurements give rational numbers as values, and the part concerned with real or complex numbers, which correspond to no empirical measurement. “Since all theorems of applied mathematics are deducible from the subsystem [of physical interpretation of the field of rational numbers]…it is only this subsystem which is verified by the interpretations.” (1978, vol. I, p. 423) So we cannot empirically confirm any claims that are properly about real or complex numbers, so we cannot empirically confirm their consistency. Hence we need Hilbert’s program of metamathematics, which, by arithmetizing the claims of mathematical languages, reduces claims of their consistency to claims in finite mathematics about the manipulations of symbols—a claim that can be confirmed empirically (see the entry on Hilbert’s program). We leave to the reader to diagnose how this separatist account fits with Reichenbach’s insistence that Bayes theorem suffices to estimate an empirical probability for theoretical claims that are not “directly” empirically confirmable.
In The Theory of Probability, modal necessity is identified with universal quantification and possibility is identified with joint existential quantification of a propositional matrix and existential quantification of its denial. At least the spirit of this account is retained in Reichenbach’s later discussions of modality. His account of modality in Elements of Symbolic Logic (1947c) was developed as a separate work in Nomological Statements and Admissible Operations (1954e), and is the basis for his discussion of possibility and necessity in his essay on freedom of the will. Completed before his death and published soon after, Nomological Statements and Admissible Operations was reissued in 1976 under the title, Laws, Modalities and Counterfactuals, with an invaluable expository foreword by Wesley Salmon. Reichenbach’s own presentation is a nearly impenetrable mix of conditions on truth, entailment, logical form, and verifiability, which surely contributed to its lack of influence. Little if any discussion of it is to be found in the decades of literature on conditionals and counterfactuals since its publication.
In contrast to Carnap, who was at work on modality at about the same time, Reichenbach understands the task of his theory to be to explain the logical form and content of subjunctives, especially of contrary-to-fact conditionals, and, at the same time, to explain how empirical evidence can warrant some counterfactuals, warrant the denial of others, and leave still others undecided. He therefore regards the ability of the theory to account for our common sense judgments of the truth or falsity of sentences involving subjunctives, counterfactuals, laws and modals as critical to its evaluation.
Reichenbach’s theory is founded on an account of natural laws. He views the logical form of all declarative sentences—modal, counterfactual or otherwise—as specifiable in an extensional first order or typed language. Modality is a property of sentences, not part of their content, and modal sentences therefore involve both a declarative sentence and a meta-language claim about that sentence. As in Carnap’s account, all modality is de dicto. Reichenbach is initially concerned with distinguishing conditionals that, as indicative sentences, are true because of the falsity of their antecedents, from true (or at least assertable) subjunctive conditionals that have false antecedents, or antecedents not known to be true. The former contain uses of propositional connectives (or “operations” in Reichenbach’s terminology) that are inadmissible. Reichenbach’s strategy is to characterize “admissible operations,” that is assertable, subjunctive conditionals, and their truth values, by their deductive relations with indicative “nomological statements.”
Fundamental or “original” nomological statements are those logically equivalent to a true sentence (with no terms that “essentially refer” to particulars) in prenex form with at least one universal quantifier and such that no logically stronger sentence in the same vocabulary is true. Derivative nomological statements are logical consequences of original nomological statements, but not all derivative nomological statements are “admissible.” To avoid conditionals true because of false antecedents (or sentences true because of irrelevant disjuncts), Reichenbach essentially requires that derivative nomological statements be the logically strongest sentences in their vocabulary that are consequences of original nomological statements. Statements are graded: Original nomological statements have grade 3, derivative nomological statements grade 2, and other statements grade 1. A counterfactual conditional can only be true—or assertible—if its antecedent has a grade at least as high as its consequent. Rather elaborate further conditions on logical form are imposed to avoid counterexamples. Counterfactuals about particulars are understood to be true if the corresponding indicative conditionals are instances of true nomological generalizations.
Modal claims of necessity are construed as indicatives combined with a meta-claim that the indicative is nomological. Possibility claims have corresponding meta-claims asserting that the denial of the indicative is not nomological. Almost as an afterthought, Reichenbach notes that quantification must be over possible as well as actual objects, but he provides no logical mechanism for specifying such de re modalities.
6. Ethics and Free Will
Reichenbach’s discussion of free action and free will is an attempt to reconcile our judgments that some actions are done freely and others are not with a scientific and materialist conception of the world. An action is free if there is a prior circumstance in which a “volition” of the actor causes the action, and in that, otherwise the same, circumstance a volition to act otherwise would with high probability have brought about a different action. Reichenbach goes to some lengths to explain just how the volition must cause the action in order to be free, but the conditions are open to fairly simple counter-examples. He also makes no attempt to relate free action to moral responsibility, or its absence to innocence.
The Rise of Scientific Philosophy (1951a), Reichenbach’s last and most successful popular book, presents his broad philosophical viewpoint in an accessible way. The English prose is more fluent than in earlier works, and occasionally almost as pithy as Russell’s. Four chapters of the book provide Reichenbach’s review of the history of philosophical pretensions to a priori knowledge in metaphysics, epistemology and ethics. Writing of Kant, Reichenbach instructs: “His cognitive a priori coincides with the physics of his time; his moral a priori, with the ethics of his social class. Let this coincidence be a warning to all those who claim to have found the ultimate truth.” (p. 61) Of Hamlet, Reichenbach writes “To be or not to be—that is not a question but a tautology.” (p. 250) Much of the remainder of the book consists of selective popular science summaries, amid simplified restatements of the views in The Philosophy of Space and Time (1928h), and Experience and Prediction (1938c). The news in the book is the extended discussion of ethics. In his contribution to the Schilpp volume (1939a) on John Dewey, Reichenbach had written at some length, and with considerable disdain, about Dewey’s ethical theory. (His personal relations with Dewey are unknown to us, but it is possible that Reichenbach knew and disapproved of Dewey’s enthusiasm for World War I.) About ethics, Reichenbach was at least as pragmatic as Dewey, but about metaethics, and in particular about the logical form of ethical sentences, he was in close accord with Charles Leslie Stevenson’s imperativism. To assert “X is good” is just to assert “I approve of X: Do so as well!” In The Rise of Scientific Philosophy he insists that ethical statements express “volitional decisions,” without truth values, that are not subject to empirical knowledge. The empirical issues of ethics are only the causal questions of relations of means to ends. Reichenbach allows a place for logic in reasoning from ethical premises to ethical conclusions, but he insists that the characteristic feature of ethical statements, and the proper conclusion of ethical reasoning, is a call to action. Whatever else they are, ethical claims are imperatives. His recommendation for resolving fundamental ethical disagreements is not philosophy or science, but “social friction.” In keeping with his politics, Reichenbach’s last practical advice was the same as Joe Hill’s: Organize! But Reichenbach’s deepest ethical injunction was implicit in his most popular book: to form beliefs, to judge them, to change them, to weigh actions, to distinguish real from merely verbal differences, by the canons of scientific philosophy.
Further Reading. In a somewhat unusual description of Reichenbach’s work, McCumber (2016) characterizes The Rise of Scientific Philosophy as “Cold War philosophy” that prudently avoids the traps of its time.
7. Reichenbach’s Influence
No complete list of Reichenbach’s doctoral students appears to be available. After coming to UCLA in 1938 he had at least six Ph.D students known to us. W. Bruce Taylor studied with him between 1949 and 1953, but we do not know about his subsequent career—he listed no academic affiliation in 1976. Melvin Maron and Norman Martin are listed by the Mathematics Genealogy Project as completing their Ph.D.s with Reichenbach in 1951 and 1952, respectively, but we know of no further record for them. Cynthia Shuster became a professor at Washington State University, from where she was fired during the McCarthy era for “corrupting the youth” by inviting Robert Oppenheimer to speak on campus. She continued her career at the University of Montana until her death. Hilary Putnam, who was at Princeton and then Harvard until his retirement, besides other important contributions less directly connected to Reichenbach, combined Reichenbach’s emphasis on learning in the limit with the theory of computation to create the foundations of computational learning theory, which remains a major theme in theoretical computer science. Until his death, Wesley Salmon, who taught at Washington State, UCLA, Northwestern, Brown, Arizona and Pittsburgh, was the philosopher who most prominently and loyally developed and defended Reichenbach’s views, especially but not exclusively his views on probability and on the justification of induction. Carl Hempel took his doctorate in Berlin with Reichenbach. After moving to the United States, he taught at Yale, Princeton and then Pittsburgh. Hempel’s work on confirmation was discussed by Reichenbach but had no connection to his own. Early in his career Hempel’s thought was more closely connected with Carnap’s logical approaches, while his later views were more closely allied with those of Thomas Kuhn, and in general his intellectual and personal relations with Reichenbach do not appear to have been close.
Some of Reichenbach’s ideas have reemerged in recent philosophy without notice of the connection. Michael Strevens’ Bigger Than Chaos (Strevens, 2003) reprises the views and arguments of Reichenbach’s doctoral thesis without the Kantian gloss. Gil Harman and Sanjeev Kulkarni’s Reliable Reasoning (2007) adopts a view of induction very close to Reichenbach’s.
Reichenbach’s views on underdetermination in physics were developed extensively by Adolf Grunbaum, but as a metaphysical rather than epistemological thesis. The issue of the conventionality of simultaneity relations has attracted a large philosophical literature. Reichenbach’s Principle of the Common Cause has attracted extensive philosophical comment, much of it devoted to purported counterexamples to a strict universal claim that Reichenbach explicitly denied. Without reference to Reichenbach, the principle was restated in the 1950s by Herbert Simon (1954) as a claim about the explanation of “spurious” correlations. Under the name “Markov condition,” in the early 1980s Reichenbach’s principle was generalized by several statisticians, most notably Terry Speed (Kiiveri & Speed, 1982), and today plays an essential role in representation and search for causal relations. We do not know whether Simon, who had been Carnap’s student at the University of Chicago, knew of Reichenbach’s ideas; the statisticians very likely did not. Perhaps not coincidentally, the senior author of this entry, who helped to develop the directed graphical representation into search and prediction procedures for causal hypotheses, studied with two of Reichenbach’s doctoral students, Schuster and Salmon. As noted above, Reichenbach anticipated formulations of probabilistic causal relevance advanced by Patrick Suppes in A Probabilistic Theory of Causality (1970), and the use of “marks” can be found in a somewhat different guise in Salmon (1984) and Dowe’s (2000) work on causality.
With the exception of discussions of the “conventionality” of simultaneity, Reichenbach’s Axiomatization seems to have had little influence on subsequent work, whereas Robb’s, rediscovered in the 1970s, has attracted some development from both philosophers and physicists. The interventionist account of causation in the Axiomatization, and more clearly in The Philosophy of Space and Time, has been developed in various ways by several 21st century writers, without explicit debt to Reichenbach. Michael Friedman (2001) has attempted to revive the quasi-Kantian viewpoint of Reichenbach’s The Theory of Relativity and A Priori Knowledge emphasizing the “relativized a priori.”
A considerable literature in linguistics has pursued Reichenbach’s ideas about the logical form and semantics of conversational language, especially about tense and the logical form of adverbial modification (see Binnick in the Other Internet Resources section below for a bibliography). Kamp (2013) lays out in some detail the enormous influence in linguistics of Reichenbach’s short comments in Elements of Symbolic Logic (pp. 289–298) that recognized the distinction between speech time, reference time and event time in the logical analysis of tense. Thus, in the past perfect (“had slept”) the event time precedes reference time, which precedes speech time, while in the simple past (“slept”) the event time coincides with reference time, while both precede speech time (see also Malatesta 2016). The subsequent analysis of reference time and its relation to event time led to the development of formal semantics that could handle a rich representation of context (e.g. Kamp’s own Discourse Representation Theory). In an ambitious book-length study of Reichenbach’s theory, McMahon (1976) takes Reichenbach’s proposal to be a progenitor of Chomsky’s theory of syntax, and attempts to supplement Reichenbach’s account with appropriate re-write rules. Reichenbach’s own discussion contains no explicit generative grammar or computational models.
8. Retrospective
Hilary Putnam (1991) has praised Reichenbach’s work as “one of the most magnificent attempts by any empiricist philosopher of this or of any other century” and called for more historical study of his work. We do not disagree, but a candid philosophical retrospective assessment of any major philosopher is bound to find flaws. As Putnam emphasizes, in the end Reichenbach tried to found epistemology and metaphysics on probability relations, but he evaded or dismissed coherent and pointed challenges from Ernest Nagel and others as to how his conception of probability could serve the purposes he required of it. Reichenbach’s work repeatedly ignored or discounted the contemporaneous or prior efforts of others that address the issues that concerned him, efforts that are in one or another way as good as, or importantly better, than his own. That is true with respect to Robb with regard to the causal construction of space-time relations; it is true with respect to Kolmogorov with regard to the theory of probability; it is true with respect to Birkhoff and von Neumann with regard to quantum logic. The effect has been to make much of Reichenbach’s best-known work something of a scientific and philosophical eddy rather than a main current. Reichenbach nonetheless was a central figure in forming the mainstream of 20th century philosophy of science as a crossdisciplinary study devoted to reconstructing and “justifying” received science rather than to proposing novel scientific frameworks or novel methodologies. At least in that fundamental respect, he remained a Kantian throughout his career.
Bibliography
Primary Literature
Chronological List of Reichenbach’s Publications
Secondary Literature
- Arntzenius, F., 1992, ‘The common cause principle’, Proceedings of the Philosophy of Science Meeting, 2: 227–237.
- Birkhoff, G., and J. v. Neumann, 1936, ‘The Logic of Quantum Mechanics’, The Annals of Mathematics (Second Series), 37(4) (Oct): 823–843.
- Carnap, R., 1928, Der Logische Aufbau der Welt, Meiner, 1998.
- –––, 1936, ‘Testability and Meaning’, Philosophy of Science, 3(4) (Oct): 419–471, and Philosophy of Science, 4(1) (Jan): 1–40.
- –––, 1960, ‘The Aim of Inductive Logic’, in E. Nagel, P. Suppes and A. Tarski (eds.), Logic, Methodology and Philosophy of Science, Stanford: Stanford University Press, 1962.
- Creary, L., 1969, A Pragmatic Justification of Induction, A Critical examination, Ph.D. thesis, Philosophy Department, Princeton University.
- Dieks, D., 2009, ‘Reichenbach and the Conventionality of Distant Simultaneity in Perspective’, in F. Stadtler, et al. (eds.), The Philosophy of Science from a European Perspective, Vienna: Vienna Circle Institute.
- –––, 2020, ‘Reichenbach, Weyl, Philosophy and Gauge’, in: S. De Bianchi and C. Kiefer (eds.), One Hundred Years of Gauge Theory (Fundamental Theories of Physics: Volume 199), Cham: Springer.
- Dowe, P., 2000, Physical Causation, Cambridge: Cambridge University Press.
- Eberhardt, F., 2011, ‘Reliability via Synthetic A Priori – Reichenbach’s Doctoral Thesis on Probability’, Synthese, 181(1): 125–136.
- Eberhardt, F. and C. Glymour, 2011, ‘Hans Reichenbach’s Probability Logic’, in D. M. Gabbay, J. Woods and S. Hartmann (eds.), Handbook of the History of Logic, Vol. 10, Amsterdam: Elsevier.
- Eddington, A.S., 1921, ‘A Generalisation of Weyl’s Theory of the Electromagnetic and Gravitational Fields’, Proceedings of the Royal Society of London (Series A), 99(697): 104–122.
- Eddington, A.S., 1924, The Mathematical Theory of Relativity, Cambridge: Cambridge University Press.
- Einstein, A., 1921, Geometrie und Erfahrung, Springer: Berlin.
- van Fraassen, B., 1979, ‘Relative Frequencies’, in W. Salmon (ed.), Hans Reichenbach: Logical Empiricist, Dordrecht: D. Reidel.
- Friedman, M., 2001, Dynamics of Reason, Stanford: CSLI Publications.
- Galavotti, M., 2011, ‘On Hans Reichenbach’s Inductivism’, Synthese, 181(1): 95–111.
- Giovanelli, M., 2016, ‘‘... But I Still Can’t Get Rid of a Sense of Artificiality’: The Reichenbach-Einstein debate on the geometrization of the electromagnetic field’, Studies in History and Philosophy of Science (Part B: Studies in History and Philosophy of Modern Physics), 54, 35–51.
- Glymour, C., 1970, ‘On Some Patterns of Reduction’, Philosophy of Science, 37(3): 340–353.
- –––, 1980, Theory and Evidence, Princeton: Princeton University Press.
- Goodman, N., 1949, ‘On Likeness of Meaning’, Analysis, 10(1): 1–7.
- Hacking, I., 1965, Logic of Statistical Inference, London: Routledge.
- –––, 1968, ‘One Problem about Induction’, in I. Lakatos (ed.), The Problem of Inductive Logic, Amsterdam: North-Holland, 44–59.
- Harman G., and S. Kulkarni, 2007, Reliable Reasoning, Cambridge, MA: MIT Press.
- Hempel, C.G., 1935, ‘On the logical positivists’ theory of truth’, Analysis, 2(4): 49–59.
- –––, 1985, ‘Thoughts on the Limitations of Discovery by Computer’, in K. F. Schaffner (ed.), Logic of Discovery and Diagnosis in Medicine, Berkeley: University of California Press, 115–122.
- Hoffman, D., 2007, ‘The Society for Empirical/Scientific Philosophy’, in A. Richardson and T. Uebel (eds.), The Cambridge Companion to Logical Empiricism, Cambridge University Press, 41–57.
- Irzik, G., 2011, ‘Hans Reichenbach in Istanbul’, Synthese, 181(1): 157–180.
- Jeffrey, R. 1983, The Logic of Decision, 2nd edition, Chicago: University of Chicago Press.
- Kamlah, A., 2013, ‘Everybody has the right to do what he wants: Hans Reichenbach’s volitionism and its historical roots’, in Milkov and Peckhaus (eds.), The Berlin Group and the Philosophy of Logical Empiricism, Dordrecht: Springer, 151–175.
- Kamp, H., 2013, ‘Deixis in discourse. Reichenbach on temporal reference’, in von Heusinger and ter Meulen (eds.), Meaning and the Dynamics of Interpretation (Current Research in the Semantics/Pragmatics Interface: Volume 29), Leiden: Brill, 105–159.
- Kiiveri, H., and T. Speed, 1982, ‘Structural analysis of multivariate data: A review’, in S. Leinhardt (ed.), Sociological Methodology, San Francisco: Jossey-Bass.
- Kries, J.v., 1886, Die Principien der Wahrscheinlichkeitsrechnung: eine logische Untersuchung, 2nd edition, Tübingen: Mohr, 1927.
- Kolmogorov, N.A., 1933, Grundbegriffe der Wahrscheinlichkeit, Berlin: Springer. English translation, Foundations of the Theory of Probability, New York: Chelsea, 1950.
- Lewin, K., 1922, Der Begriff der Genese in Physik, Biologie und Entwicklungsgeschichte, Berlin: Springer.
- Lewis, C.I., 1929, Mind and the World Order, New York: Dover Publications, 1991.
- –––, 1946, An Analysis of Knowledge and Valuation, La Salle: Open Court.
- –––, 1952, ‘The Given Element in Empirical Knowledge’, The Philosophical Review, 61(2): 168–172.
- Lutz, L. and A.T. Tuboly (eds.), 2021, Logical Empiricism and the Physical Sciences, New York: Routledge.
- Malatesta, M., 2016, ‘Tenses and Temporality in Reichenbach’s Thought’, in The Concept of Time in Early Twentieth-Century Philosophy, Cham: Springer, pp. 217–228.
- Masson, J., 1986, The Complete Letters of Sigmund Freund to Wilhelm Fleiss, 1887–1904, Cambridge, MA: Harvard University Press.
- McCumber, J., 2016, The Philosophy Scare: The Politics of Reason in the Early Cold War, Chicago: University of Chicago Press.
- McMahon, W., 1976, Hans Reichenbach’s Philosophy of Grammar, The Hague: Mouton.
- Milkov, N., 2013, ‘The Berlin Group and the Vienna Circle: Affinities and Divergences’, in Milkov and Peckhaus (eds.), The Berlin Group and the Philosophy of Logical Empiricism, Dordrecht: Springer, 3–32.
- Milmed, B.K., 1961, Kant & Current Philosophical Issues, New York University Press.
- Mises, R.v., 1919, ‘Grundlagen der Wahrscheinlichkeitsrechnung’, Mathematische Zeitschrift, 5: 52–99.
- Nagel, E., 1936, ‘Critical Notices’, Mind, 45(180): 501–514.
- –––, 1938, ‘Principles of the theory of probability’, in R. Carnap, C. Morris, and O. Neurath (eds.), Foundations of the Unity of Science, Chicago: University of Chicago Press.
- Neumann, J.v., 1932, Mathematical Foundations of Quantum Mechanics, R.T. Beyer (transl.), Princeton: Princeton University Press, 1996.
- Padovani, F., 2008, Probability and Causality in the Early Works of Hans Reichenbach, Ph.D. thesis, University of Geneva.
- –––, 2011, ‘The Concept of Probability in the Mathematical Representation of Reality’, HOPOS: The Journal of the International Society for the History of Philosophy of Science, 1(2): 344–347.
- –––, 2011, ‘Relativizing the Relativized A Priori: Reichenbach’s axioms of coordination divided’, Synthese, 181(1): 41–62.
- –––, 2013, ‘Genidentity and Topology of Time: Kurt Lewin and Hans Reichenbach’, in Milkov and Peckhaus (eds.), The Berlin Group and the Philosophy of Logical Empiricism, Dordrecht: Springer, 97–122. (See also Padovani, 2008, Ch. 5.)
- –––, 2015, ‘Reichenbach on Causality in 1923: Scientific inference, coordination, and confirmation’, Studies in History and Philosophy of Science (Part A), 53: 3–11.
- –––, 2017, ‘Coordination and Measurement: What we get wrong about what Reichenbach got right’, in M. Massimi, J.-W. Romeijn, and G. Schurz (eds.), EPSA15 Selected Papers (The 5th conference of the European Philosophy of Science Association in Düsseldorf), Cham: Springer, pp. 49–60.
- Peijnenburg, J, and D. Atkinson, 2011, ‘Grounds and Limits: Reichenbach and Foundationalist Epistemology’, Synthese, 181(1): 113–124.
- Poincaré, H., 1902, La Science et l’hypothèse, Paris: Flammarion, 2004. English translation Science and Hypothesis, London: Walter Scott Publishing, 1905.
- –––, 1912, Calcul des probabilités, Paris: Gauthier-Villars.
- Popper, K., 1934, The Logic of Scientific Discovery, London: Routledge, 2002.
- Poser, H., and U. Dirks (eds.), 1998, Hans Reichenbach, Philosophie im Umkreis der Physik, Berlin: Akademie Verlag.
- Psillos, S., 2011, ‘On Reichenbach’s Argument for Scientific Realism’, Synthese, 181(1): 23–40.
- Putnam, H., 1991, ‘Reichenbach’s Metaphysicial Picture’, Erkenntnis, 35: 61–75.
- Quine, W.V.O., 1951, ‘Two Dogmas of Empiricism’, The Philosophical Review, 60: 20–43.
- Reichenbach, M., 1994, ‘Erinnerung und Reflexionen’, in Dannenberg, Kamlah & Schäfer (eds.) Hans Reichenbach und die Berliner Gruppe, Braunschweig: Vieweg, pp. 7–17.
- Robb, A.A., 1914, A Theory of Time and Space, Cambridge: Cambridge University Press.
- –––, 1921, The Absolute Relations of Time and Space, Cambridge: Cambridge University Press.
- Russell, B., 1914, Our Knowledge of the External World, London: Allen & Unwin.
- –––, 1945, ‘Logical Positivism’, Polemic, 1: 6–13.
- –––, 1948, Human Knowledge, Its Scope and Limits, New York: Simon Schuster, London: Allen & Unwin.
- –––, 1897, An Essay on the Foundations of Geometry, New York: Dover, 1956.
- Ryckman, T., 2005, The reign of relativity; Philosophy in Physics 1915–1925, Oxford: Oxford University Press.
- –––, 2007, ‘Logical Empiricism and the Philosophy of Physics’, in A. Richardson and T. Uebel (eds.), The Cambridge Companon to Logical Empiricism, Cambridge: Cambridge University Press.
- Salmon, W., 1977a, Introduction in Collected Works, in Reichenbach (1977a), Volume 1.
- Rynasiewicz, R., 2003, ‘Reichenbach’s ε-Definition of Simultaneity in Historical and Philosophical Perspective’, in Stadler (ed.), The Vienna Circle and Logical Empiricism, Berlin: Springer, pp. 121–129.
- –––, 2005, ‘Weyl vs. Reichenbach on Lichtgeometrie’, in Kox and Eisenstaedt (eds.), The Universe of General Relativity, Berlin: Springer, pp. 137–156.
- Salmon, W., 1977b, ‘Laws, Modalities and Counterfactuals’, Synthese, 35: 191–229.
- –––, 1979, Hans Reichenbach, Logical Empiricist, Dordrecht: D. Reidel.
- –––, 1984, Scientific Explanation and the Causal Structure of the World, Princeton: Princeton University Press.
- Salmon, W. (ed.), 1994, Logic, Language, and the Structure of Scientific Theories: Proceedings of the Carnap-Reichenbach Centennial (University of Konstanz, May 21–24, 1991), Pittsburgh: University of Pittsburgh Press; Konstanz: Universitätsverlag Konstanz.
- Schickore, J. and F. Steinle, 2006, Revisiting discovery and justification: historical and philosophical perspectives on the context distinction, Berlin: Springer.
- Schilpp, A., 1939. The Philosophy of John Dewey, Evanston: Northwestern University Press.
- Schrödinger, E., 1924, ‘Anmerkungen zum Kausalproblem’, Erkenntnis, 3 (1932): 65 (appended to Reichenbach 1932d); reprinted in Reichenbach (1978), Volume II.
- Simon, H., 1954, ‘Spurious Correlation: A Causal Interpretation’ Journal of the American Statistical Association, 49(267) (Sep): 467–479.
- Strevens, M., 2003, Bigger than Chaos, Cambridge, MA: Harvard University Press.
- Stumpf, C., 1892a, ‘Über den Begriff der mathematischen Wahrscheinlichkeit’, Sitzungsberichte der philosophisch-historischen Klasse der Bayerische Akademie der Wissenschaft, 1 (1893): 37–120.
- –––, 1892b, ‘Über die Anwendung des mathematischen Wahrscheinlichkeitsbegriffes auf Teile eines Continuums’, Sitzungsberichte der philosophisch-historischen Klasse der Bayerische Akademie der Wissenschaft, 4 (1893): 681–691.
- Suppes, P., 1970, A Probabilistic Theory of Causality, Amsterdam: North Holland.
- Verhaegh, S., 2020, ‘Coming to America: Carnap, Reichenbach and the Great Intellectual Migration. Part II: Hans Reichenbach’, Journal for the History of Analytical Philosophy, 8(11), first online 18 December 2020. doi:10.15173/jhap.v8i11.4562
- Weyl, H., 1924, ‘Rezension von: H. Reichenbach: Axiomatik der relativistischen Raum- Zeit Lehre’, Deutsche Literaturzeitung, 45: 2122–2128.
- –––, 1927, Philosophie der Mathematik und Naturwissenschaft, 2nd edition, Philosophy of Mathematics and Natural Science, Princeton: Princeton University Press, 1949.
- Wilholt, T., 2012, ‘Conventionalism: Poincaré, Duhem, Reichenbach’, in Brown (ed.) Philosophy of Science: The Key Thinkers, London: Bloomsbury Publishing, 32–52.
- Woodward, J., 2003, Making Things Happen, Oxford: Oxford University Press.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
We include the links below for further reference, but note that some of the online resources contain some factual errors in content. We did our best to avoid such errors here, but welcome any comments and corrections. We also welcome suggestions for further links.
- The Hans Reichenbach Papers, Archives of Scientific Papers, University of Pittsburgh.
- Binnick, R., Project on the Bibliography of Tense, Verbal Aspect, Aktionsart, and Related Areas, see papers related to Reichenbach’s work on language.
- Hans Reichenbach, entry in Wikipedia.
- Hans Reichenbach, entry in the Internet Encyclopedia of Philosophy.
- Hans Reichenbach, biography of Reichenbach in MacTutor (University of St. Andrews).
- Hans Reichenbach, Mathematical Genealogy Project.
Acknowledgments
We would like to thank Flavia Padovani for her comments and further references on a draft and the update of this entry, as well as the anonymous reviewer(s). We welcome further corrections and comments.


